医学物理士認定試験合格体験記 Part1

こんにちは!お久しぶりです!
長らく更新が途絶えていましたが、いろいろと落ち着いたので久々のブログです笑
この度、医学物理士認定試験に無事合格したので、合格体験記を残しておきたいと思います。
私自身はスタンダードな経路ではないと思うので、参考になるかはビミョーですが良かったら読んでみてください。
1.医学物理士認定試験の概要
医学物理士認定試験の詳細については、医学物理士認定機構のホームページを参照していただければと思います。
試験内容を簡単にまとめると、
(1)多肢選択式 物理工学系
(2)多肢選択式 医学生物系
(3)記述式 物理工学系
の3つがあります。
合格基準は公開されていませんが、合格率が毎年約30%で変動がほとんどないので、上位3割が合格とされているようです。
色々と見た感じでは、多肢選択式と記述式それぞれ7割以上取れていれば十分合格できるのではないかと予想されます。
あくまで参考程度ですが、私自身は手応え的に7〜8割は取れたのではないかと思っています。
勉強の進め方を紹介する前にまずは、事前に必要な準備を確認していきましょう。
2.事前準備
医学物理士認定試験にはそこそこの受験資格が必要になります。
現在、基本的には以下の受験資格が課されています。
日本医学物理学会の正会員で、次の各号のいずれかを満たす者に受験資格を与える。
(1) 機構認定の医学物理教育コースに 1 年以上在籍または修了した者
(2) 理工学系修士以上の学位を有し(取得見込みを含む)、医学物理士認定制度施行細則(以下、「細則」という)に定める業績評価点 5 単位以上を有する者
(3) 放射線技術系修士以上の学位を有し(取得見込みを含む)、細則に定める業績評価点 5 単位以上を有する者
(4) 医学系研究科に設置された医学物理に関する課程の修士以上の学位を有し(取得見込みを含む)、細則に定める業績評価点 5 単位以上を有する者
(5) 学歴によらず医学物理の発展に寄与したと特に認められる者
また、特例措置として以下の受験資格も認められています。
(1) 平成 24 年度までに理工学系学士の学位を取得し、医学における経験年数 3 年以上の者
(2) 平成 24 年度までに放射線技術系学士の学位を取得し、医学における経験年数 2 年以上の者
(3) 平成 22 年度までに診療放射線技師免許を取得し、医学における経験年数 5 年以上の者
(4) 平成 22 年度までに、医師または歯科医師以外で医学または歯学博士の学位を取得し、医学における経験年数 1 年以上の者
実際のところは分かりませんが、おそらく受験資格の(1)〜(4)および特例措置の(2)あたりの方が多いのではないかと思います。
私自身は認定コースではない放射線技術系の大学院に所属しており、受験資格としては(3)で出願しました。
このため、準備が必要となったのは、
①日本医学物理学会の正会員
②業務評価点5点
の2つです。
それぞれ説明していきます。
①日本医学物理学会の正会員
まず、受験時に日本医学物理学会の正会員である必要があります。
注意が必要なのは“正会員”という点です。
大学院生は学生会員または未入会の方が多いと思うので、学生会員の方は正会員への移行、未入会の方は正会員の申請が必要となります。
②業務評価点5点
受験に必要な業務評価点については医学物理士認定試験施行規則において、以下のように定められています。
規程第 9 条に定める業績評価点は、前々年度の 4 月 1 日から受験年度の 9 月 30 日まで の期間の合計とする。
前項の業績評価点は、別表のカテゴリーIIおよびIIIの項目について加算できるものとする。
受験年度の前々年度4月1日から受験年度の9月30日までの約2年半の間に業務評価点5点を取得する必要があります。
対象となる業務評価点はカテゴリーII(医学物理士業務に関する講習会等への参加)、カテゴリーIII(医学物理学に関する学術大会等への参加、医学物理学に関する学術論文・著書)です。
詳細は医学物理士認定試験施行規則を参照してください。
試験対策も含めてミニマム講習会を受講される方が多いと思いますが、私は医学物理学会の教育セミナーを受講しました。
詳しくは後述しますが、自分の興味と必要なポイント、かかるお金を考慮して選択しました。
比較的受験申し込み直前まで対応可能だとは思いますが、出来るだけ早めに準備しておくことをお勧めします。
おまけ:学生には重要なおカネの話
医学物理士認定試験の受験にはなかなかのお金がかかります。
最低限必要な費用は以下の通りです。
1)日本医学物理学会正会員
入会費:4,000円
年会費:10,000円
計:14,000円
2)受験料
20,000円
3)業務評価点
カテゴリーII
5,000〜20,000円
カテゴリーIII
学会によって異なる
総計:40,000〜54,000円
カテゴリーIIについては、おそらく最も費用がかからないもので5,000〜6,000円(非会員)程度だと思います。日本医学物理学会の学生会員であれば1,000円のものもありますが、学生会員の年会費が4,000円なので結果的に同程度の費用と考えられます。
私は偶然、医学物理学会の教育公演セミナーが面白そうな内容だったので受講しましたが、特になければミニマム講習会を受講しようと考えていました。
ミニマム講習会は認定試験の問題集(解答付き、解説なし)込みの講習会であり、模擬試験なども行われるので、認定試験対策として受講される方も多いと思います。
ただし、受講料が物理工学系または医学生物系の片方で20,000円かかるのでなかなかの出費ですよね。
また、医学物理士認定試験記述式対策講習会もありますが、この講習会には業務評価点が割り振られていないので注意しましょう。
こういったセミナー、講習会などは自分の興味に沿って受講することが望ましいと思いますが、学生にとってはそれなりの出費になると思うので、計画的に業務評価点を取得しておきましょう。
3.勉強スケジュール
さて、事前準備を整理したところで勉強の進め方について書きたいと思います。
各科目、形式ごとの詳細については次の記事で書こうと思っているので、ここでは簡単なスケジュールのみ示します。
受験までにやったこと
試験対策としては
①多肢選択式(物理工学系・医学生物系)の解答・解説作成
②医学物理学教科書シリーズの通読
を行いました。
① 多肢選択式の解答・解説作成
医学物理士認定試験は解答が公表されておらず、もちろん解説付きの問題集などもないため解説もありません。
このため自力で解答・解説を作成しました。
解答・解説を作成する過程で問題に関する周辺知識もつけることができるので、非常に有用だったと思います。
しかしながら、なかなかの時間を必要とするので、社会人の方や研究が忙しくて手が回らない方は群馬大学の試験対策サイトをお勧めします。
まれにバグや解答の間違いが見られますが、解答と簡単な解説がついているので、スキマ時間を利用して対策が可能です。
②医学物理学教科書シリーズの通読
医学物理学教科書シリーズは日本医学物理学会から出版されている教科書であり、医学物理士認定試験対策に非常に有用です。
現在、以下の7冊が出版されています。
・放射線物理学
・放射線診断物理学
・核医学物理学
・放射線治療物理学
・放射線計測学
・画像・情報処理
・医療放射線防護学
このシリーズは基本的に記述式対策として使用したので、記述式の科目のみ通読しました。
それ以外の教科書についても、先述した解答・解説作成のために参照しました。
科目にもよりますが、ここ数年は記述式試験の出題内容はこの教科書からのものが多いため、細かく覚えていなくても一度通読しておく価値はあると思います。
実際に今年の試験においても教科書を読んでいて問題に出来そうだなと思っていたところが出題されていました。
具体的なスケジュール
では、具体的なスケジュールを示します。
2020年
4月〜6月 多肢選択式解答作成
7月〜1月 ほとんど進まず😱
2021年
2月〜3月 多肢選択式解答作成
4月〜5月 医学物理学教科書通読
6月〜7月 就活など
8月 医学物理学教科書通読
9月 多肢選択式解き直し、記述式
元々、医学物理士を受けようと考えたのは大学院1年の始めです。
大学院入学早々コロナ禍に突入し、大学にも入れない期間がしばらくあったので、時間を無駄にしないように何か勉強しようと思い、勉強し始めました。
しかし、その後は研究やアルバイトなどでそれなりに忙しく、ほとんど進められませんでした。時間がなかったわけではなかったので、単に私の怠惰ですね笑
今年の2月あたりからはちょろちょろと時間をとって解答作成を進め、4月あたりには2010年〜2020年までの11年分の解答を完成しました。
これ以降は医学物理学教科書シリーズの通読に費やしました。途中就職活動も挟んだので、空いた時間を使って少しずつ進めていきました。
9月上旬あたりでやっと一通り読み終えられたので、そこからは多肢選択式の解き直しや記述式の過去問を解いたりしました。
記述式に関しては過去問がそのまま出題されることは少ないので、参考程度にかいつまんで解きました。
4.総括
多肢選択式に関しては、2020年度の問題を何も見ずに解いて物理工学系および医学生物系で7割以上取れていたので大丈夫かなと思っていましたが、記述式に関しては運要素が強めなので少し不安でした。
実際の試験では3問中2問完答、1問は小問2つでミスという感じで、それなりに余裕をもって合格できたのではないかと思います。
医学物理士は主に放射線治療系の資格として認識されていると思いますが、問題は治療に限らず幅広く出題されます。
このため、他の認定資格とは異なり、実際の業務経験がそこまで関わらない資格と言えます。
確保できる勉強時間が多い学生が有利になると思うので、受ける気があるなら学生のうちに合格することをお勧めします。
次回は各形式、各科目について少し詳しく書いていきたいと思います!
ではまた!
医学物理士認定試験問題研究①平均情報量

こんにちは!
今回は医学物理士認定試験で出題される内容から私が独学で勉強したことをいくつかまとめていきたいと思います。
ただテーマとなる内容は私が気になった内容にかなり偏ります。
全科目を均等に網羅するものでは無いので、ご了承ください!
医学物理士認定試験では診療放射線技師国家試験より専門的な内容も増えるので誤りを含む可能性も高くなると考えられます。
誤りに気づいた方は遠慮せずご指摘ください。
では早速、今回は「平均情報量」について書いていきます。
平均情報量は情報理論に含まれる内容であり、馴染みが無い方も多いかと思います。
まずは基本となる情報量の概念から確認していきます。
情報量とは
情報量は以下のように定義されています。
確率
で生起する事象が起きたことを知ったときに、得られる情報量
を
と表す。
全く情報理論に触れたことが無い方は「はて、何のことやら?」という状態かと思います。
この式を眺めてみると、情報量はその事象が起こる確率が小さいほど大きくなる値であることがわかります。
これがどういったことを表しているのか、少し考えてみましょう。
例として、サイコロを投げて出た目を当てるゲームを扱います。
まず出た目に関して全く情報がない場合、すべての事象(1~6の目が出る)に対して成り立つ情報しかないため、確率は1と考えます。

よって得られる情報量は
となります。
情報が全くないわけですから、情報量は0。当たり前ですね笑
では、次に出た目が奇数であるという情報を得た場合を考えます。

出た目は1、3、5の3通りに絞られますから確率はとなり、その情報量は
となります。
先ほどよりも情報量が大きくなりましたね。
では最後に出た目が奇数かつ3以下である場合を考えてみましょう。

このとき出た目は1と3の2通りに絞られますから、確率はとなり、その情報量は
となります。
より、2つ目の場合より情報量が大きくなっています。
この例から情報量は起きた事象の確率が小さいほど大きくなるものであることが分かります。
これはその事象の起きる確率が小さいほど、その事象が起きたという情報の価値が大きくなるという風に解釈することができます。
今の例で言うと、より選択肢(サイコロの目)を絞れる方が情報量が多いということですね。
また、この情報量は画像などのデータ量としても考えることができます。
画像に限らず、コンピューターで扱われるデータは全て0か1の2つの数字の組合せで表現され、最小単位はbitです。
例えば画像の諧調数が256のとき、1画素当たりのデータ量はより、8bitになります。
(2進数の表現については省略します。)
画素値は256通りあり、そのうちの1つが得られたわけですから、その情報量は、
[bit]
となり、データ量と一致します。
先ほどの例では対数の底を特に指定していませんでしたが、情報量をbit単位で表す場合、底は2とする必要があります。
このため、基本的に底は2が用いられます。
これで情報量の概念をだいたい理解できたのではないでしょうか。
では、続いて平均情報量(情報エントロピー)についてまとめていきます。
平均情報量とは
平均情報量(情報エントロピー)は以下のように定義されています。
個の互いに排反な事象
が起こる確率を
とする(ただし、
)。
このとき、得られる平均情報量
は、
と表せる。
先程と同様に式を見てみると、ある事象が起きた時に得られる情報量にその事象が起きる確率をかけたものを足し合わせたものになっています。
これは何を示すのでしょうか?
得られる情報量にその事象が起きる確率がかけられているので、平均情報量は名前の通り、平均してどのぐらいの情報量が得られるのかを示していると考えることができます。
統計学でいう期待値と同じですね。
期待値があまりピンとこないという方は少し調べてみてください。
とりあえず平均情報量についてはこの程度で大丈夫でしょう。
では早速、問題を解いてみます!
問題演習①
問題は2018年度問題71です。
問題71 排反する2つの事象の生起確率がそれぞれ0.4と0.6であるとき、2つの事象のエントロピー[bit]はどれか。
ただし、
および
とする。
a.-2.6
b.-0.94
c.0.10
d.0.94
e.2.6
(2018年度医学物理士認定試験多肢選択式物理工学系より引用)
ぜひ答えを見ずに一度解いてみてください。
解けたでしょうか?
解答としては以下のようになります。
2つの事象の生起確率をそれぞれ、
とすると、エントロピー(平均情報量)は、
であり、、
を代入すると、
と求められます。
よって解答はdです!
結構簡単に解けたのではないでしょうか?
では次にこの問題を解いてみましょう。
問題演習②
問題は2014年度問題61です。
問題61 4つの文字A、B、C、Dからなるデータの平均情報量がもっと多いのはどれか。
ただし、
、
、
、
はそれぞれの文字の出現確率とする。
(2014年度医学物理士認定試験多肢選択式物理工学系より引用)
どうでしょうか?
事前知識がなく、このブログしか読んでいない人はほぼほぼ解けないかと思います。
おそらく立式して計算していく途中で、
「あれ?計算できなくない??」
となったのではないでしょうか。
では、実際に計算してみましょう。
まずはaからやってみます。
より、
aの選択肢は問題なく計算できました。
では続いてbを計算してみましょう。
おそらく皆さんお気づきかと思いますが、先ほど計算がうまくいったのは確率が2の累乗だったからです。
確率が2の累乗でない場合、電卓なしに対数の計算をすることはできません。
これでは平均情報量の比較ができません。
しかし、実はこの問題はある定理を知っているだけで秒殺できる問題です。
その定理について理解していきましょう。
平均情報量に関する定理
平均情報量について、以下のような定理が成り立ちます。
事象の数を
、それぞれの確率を
、
、…、
とするとき、
で
は最大となり、その値は
である。
この定理はもちろんちゃんと証明することができますが、とりあえずは感覚的に理解しましょう。
初めの方で説明したように情報量は確率が小さい事象が起きたときに大きくなります。
しかし、起きる確率が小さいわけですから、その事象が起きたという情報が得られる可能性も小さくなります。
この両方のバランスが取れていないと平均情報量は最大になりません。
それが全ての事象の確率が等しいときというわけです。
また、平均情報量は情報エントロピーとも呼ばれます。
エントロピーは主に熱力学や統計力学の分野で登場する概念であり、大雑把に言うと乱雑さやばらつきを示すものです。
全ての事象の確率が等しい場合、次に起こる事象には全く傾向がなく予測がしにくいという風に解釈できます。
こう考えると、すべての事象の確率が等しい時にエントロピーが最大になるという考え方の方がしっくりきやすいかもしれませんね。
こうはいったものの、数式を用いてはっきりさせたいという方のために、一応定理の証明*1も書いてみました。
なかなかややこしいですが、気になる方は読んでみてください。
さて、この定理を用いることで先程の問題がすぐに解けてしまいます!
では、解答にいきましょう。
定理より、となるとき平均情報量は最大となるため、
となるaが解答です。
まったく計算せずに解くことができました笑
まとめ
今回の平均情報量の定理のように、それを知らないだけで簡単な問題が超難問になってしまうという場合があります。
特に独学で勉強していく場合は、すべての分野を一通り学習するというのはなかなか難しいのでこういったことが起こりがちです。
勉強を進めていくうえでわからない言葉や概念が出てきたときは、問題を解くために必要な情報だけを調べるのではなく、もう少し突っ込んで勉強してみるのも良いかもしれませんね。
この医学物理士認定試験問題研究は今後もちょこちょこ更新していく予定なので、ぜひお楽しみに!
ではまた!
<補足>
国試の難問?⑥(第67回診療放射線技師国家試験午前39)
こんにちは!
お久しぶりの国試の難問?シリーズです!
今回は電子線の線量分布についての問題を扱っていきます。
電子線治療は適応の少なさからか、あまり詳しく習わないことが多いような気がします。
しかし、X線による治療とは性質が異なる部分も多々あるので押さえておくと良いと思います。
少し物理学の理解が必要になるので、ややこしいところもあると思いますが、ぜひ最後まで読んでみてください!
問題解説
問題は第67回午前39です。
39 電子線の線量分布について誤っているのはどれか。
1.斜入では表面線量が増加する。
2.半影は低エネルギーで大きくなる。
3.エネルギーの増加とともに表面線量が低下する。
4.エネルギーの増加とともに制動放射が増加する。
5.照射野サイズが小さくなると表面線量が増加する。
(第67回診療放射線技師国家試験より引用)
正答を選ぶこと自体はそこまで難しくありませんが、他の選択肢の正誤を判断するのが少し難しいと思います。
では、各選択肢について吟味していきましょう。
1.電子線の斜入
まずは電子線の斜入に関する選択肢です。
1.斜入では表面線量が増加する。
まず電子線の特徴として、側方散乱が多いことが挙げられます。
入射方向に垂直な面に入射する場合、このような分布になると仮定します。

このように仮定すると、電子線が斜入した場合以下のような分布になると考えられます。

表面から同じ深さの点で比較すると、斜入した場合は隣接する点に入射した電子線の側方散乱による線量付与が加わるため、表面線量が大きくなると考えることができます。
2.電子線の半影
次は電子の半影についての選択肢です。
2.半影は低エネルギーで大きくなる。
先程述べた電子線の側方散乱はエネルギーが低いほど顕著になります。

エネルギーが高いほど直進性が高く、側方散乱が少なくなるということですね。
低エネルギーでは側方(照射野の外側)への散乱が多いわけですから、照射野(線量分布)の半影が大きくなると言えるでしょう。
3.PDDのエネルギー依存性
続いてPDD(深部線量百分率)のエネルギー依存性についての選択肢です。
3.エネルギーの増加とともに表面線量が低下する。
PDDは以下のようなエネルギー依存性があります。

図を見てわかるようにエネルギーが高くなるほど、表面線量が高くなっているように見えます。
ただ、少し注意しなければならないのはPDDは最大線量を100%とした場合のある深さにおける線量の比を示すものであることです。
つまり、この選択肢中における「表面線量の低下」というのは最大線量の深さ(最大深、基準深)に対する表面の線量の比が小さくなるという意味と解釈できます。
エネルギーが高くなるほどPDDは大きくなっていますから、この選択肢は誤りと考えられます。
ここで、なぜこのようなことが起こるか、もう少し考えてみましょう。
前述した通り、低エネルギーの電子線は側方散乱が大きいため、深さ方向の線量変化が急峻になります。
図で示すとこのような感じですね。

電子線においても表面から最大深までのビルドアップ領域が存在します。
低エネルギーの場合は側方散乱が大きいため、表面と最大深の線量比が大きくなると考えられます。
したがって、PDDのように最大深で規格化する(最大深の線量を100%とする)と、「表面線量が低くなる」と言えます。
逆に高エネルギーの電子線の場合、低エネルギー電子線と比較して側方散乱が少なく、直進性が高いためビルドアップ領域の線量勾配は小さくなります。
このため、表面と最大深の線量はあまり変化しません。
PDDのエネルギー依存性はこのように考えておけば良いでしょう。
4.制動放射のエネルギー依存性
制動放射のエネルギー依存性は放射線物理学でもよく問われる内容なので、そこまで難しくないと思います。
4.エネルギーの増加とともに制動放射が増加する。
電子と物質の相互作用(エネルギー損失)を示す以下のような図をよく見かけるかと思います。
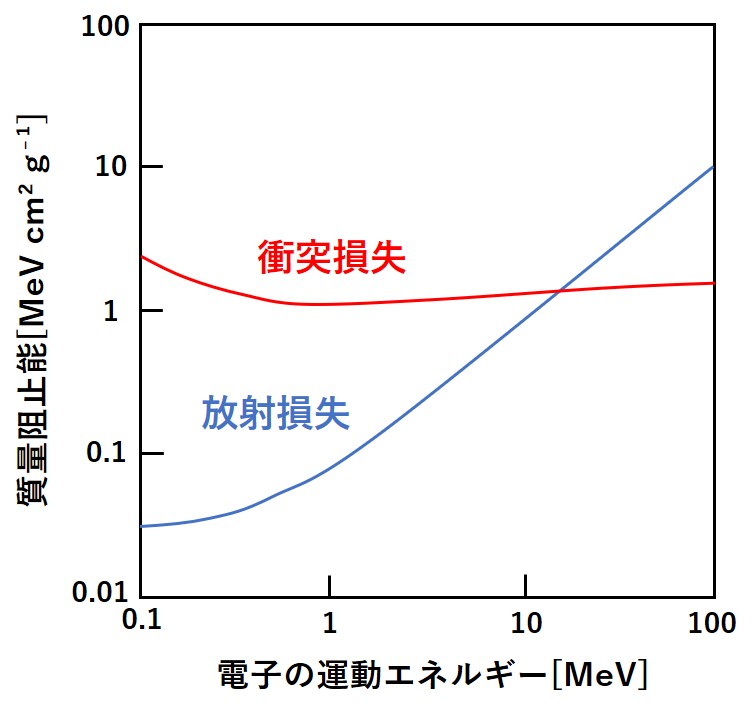
この図よりエネルギーが高くなるほど制動放射(放射損失)の割合が高くなることが分かります。
また、電子線のエネルギー損失のうち、衝突損失と放射損失の比には以下のような関係があります。

:エネルギー、
:原子番号
この関係からもエネルギーが高いほど、放射損失が大きい、すなわち制動放射が増加することが分かるでしょう。
5.PDDの照射野サイズ依存性
最後はPDDの照射野サイズ依存性についての選択肢です。
5.照射野サイズが小さくなると表面線量が増加する。
後程述べますが、これは少し微妙な選択肢です。
まずは照射野サイズがPDDにどのような影響を与えるか考えてみましょう。
照射野サイズが十分に大きい場合、照射面積が大きい分、側方からの電子フルエンス(散乱)による線量付与があるため、照射野サイズが小さい場合に比べて線量が持ち上げられると考えられます。
これにより照射野サイズが十分に大きい場合には表面と最大深の線量の差が相対的に大きくなるため、表面のPDDは小さくなると考えられます。
逆に照射野サイズが小さい場合には、側方からの電子フルエンスが少なく、表面のPDDは大きくなる(最大深と表面の線量の差が小さくなる)と考えられるでしょう。
この選択肢も3の選択肢と同様にPDD基準であり、実際の線量の値でないと考えればある程度納得できます。
ただ、教科書や参考書などのグラフを見ても表面におけるPDDの差もそこまで見られないものが多く、照射野サイズが小さいほど表面線量が増加すると明言されたものも見つからなかったので少し微妙な選択肢だと思います。
(明確な根拠が分かる方はぜひ教えてください!)
ここまで説明してきた通り、解答は3になります!
前提を理解していないと何とも言えない選択肢があり、少し難しい問題だったのではないでしょうか。
私自身もはっきりと言いきれない部分が少しあるので、もし誤りや不正確な部分がありましたらぜひ教えてください!
ではまた!
主任者試験を極める②(H27 第1種放射線取扱主任者試験 物理学 問17)
こんにちは!
今回は前回と同じく物理学の問題です。
物理学の出題ですが、どちらかというと計測学の問題です(前回の問題もそうでしたね)。
問題は平成27年度物理学問17です。
問17 NaI(Tl)γ線スペクトロメータにより、エネルギー未知のγ線の波高分布スペクトルを測定したところ、全吸収ピークが600チャネルに、コンプトンエッジが400チャネルに観測された。この場合のγ線エネルギー[keV]はいくらか。ただし、このスペクトロメータの零点調整はなされている。
1.320
2.511
3.662
4.835
5.1,170
公益財団法人原子力安全技術センター
(https://www.nustec.or.jp/syunin/syunin05.html)
より引用
この問題を理解するためには光子と物質の相互作用とスペクトル解析の基礎を知っておく必要があります。
基礎の確認をかなり丁寧に行っていくので、少し長くなりますがしっかり理解したい人はぜひ最後まで読んでみてください。
(理解できているところは適宜飛ばして読んでいただいて構いません)
では早速、基礎事項の確認から始めましょう。
基礎の確認
まず光子と物質の相互作用を簡単に復習してから、スペクトル解析の基礎を理解するという流れで書いていきます。
光子と物質の相互作用
光子と物質の相互作用は主に弾性散乱・光電効果(吸収)・コンプトン散乱・電子対生成・光核反応の5つがあります。
この中でも放射線計測で重要となることが多いのは光電効果・コンプトン散乱・電子対生成の3つです。
それぞれの相互作用について見ていきますが、今回の問題と関連する部分に絞って説明するのでこれだけ押さえておけば十分というわけではありません。
必要に応じて教科書や参考書などをじっくり読んでみてください。
光電効果
光電効果は光子が原子の軌道電子にエネルギーを与えることにより、軌道電子が飛び出すという現象です。

この軌道電子が飛び出すためには、少なくとも光子が軌道電子の結合(束縛)エネルギー以上のエネルギーを持っている必要があります。
このため、飛び出す軌道電子(光電子)のエネルギーは、光子のエネルギーを
、軌道電子の結合エネルギーを
とすると、
と表せます。
後程もう少し詳しく述べますが、光電効果により軌道電子が飛び出すとその原子の軌道には空席が生じることになります。
この空席に外殻から軌道電子が遷移してくることにより、軌道の結合エネルギーの差と同じエネルギーをもつX線(特性X線)やオージェ電子の放出が競合して起こります。
この過程も重要になるので押さえておきましょう。
コンプトン散乱
コンプトン散乱は光子と軌道電子が衝突することによって電子と散乱光子が生じる現象です。

教科書・参考書では光子と自由電子の衝突と書かれていることが多いですが、これは単に入射光子のエネルギーが軌道電子の結合(束縛)エネルギーが無視できるぐらいに大きい場合を仮定しているためと理解できます。
このコンプトン散乱で放出される電子(コンプトン電子)と散乱光子のエネルギーは衝突前後のエネルギー保存則および運動量保存則から導くことができますが、計算がなかなか長くなってしまうので今回は結果のみ使用します。
先程と同じく、入射光子のエネルギーを、コンプトン電子のエネルギーを
、散乱光子のエネルギーを
とすると、
:電子の静止質量エネルギー
:散乱光子の散乱角
と表せます。
さすがに試験の時にいちいちこの式を導出していると大変なので覚えてしまうことをオススメします。
式を見てもらえば分かる通り、2式は分母の一部だけが異なっています。
この辺に注目して覚えてもらえればと思います。
また、これらの式には散乱光子の散乱角が含まれています(コンプトン電子の散乱角ではないので注意しておきましょう!)。
この散乱角が変わることにより、それぞれのエネルギーも変わってくるということですね。
電子対生成
電子対生成は光子の入射により電子‐陽電子対が生成される現象です。

静止質量エネルギーが同じ電子と陽電子(0.511 MeV)を生成するため、電子対生成が起こるためには1.022 MeVのエネルギーが必要になります(エネルギーと質量の等価性)。
放出される電子、陽電子のエネルギーは入射光子のエネルギーからそれぞれの静止質量エネルギーの和(1.022 MeV)を引いて残ったエネルギーを分け合うことになります。
この運動エネルギーは電子、陽電子に等分されるわけではないので、連続分布します。
また、電子対生成により生じた陽電子と他の電子が対消滅を起こすことで0.511 MeVの消滅放射線が正反対の方向に2本放出されます。

これも後程重要になるので押さえておきましょう。
まとめ
ここまで各相互作用について簡単に説明してきましたが、これら相互作用はそれぞれが独立して起こるものではありません。
このエネルギーでは光電効果のみ、このエネルギーではコンプトン散乱のみというものではないということです。
もちろんエネルギーが高くなるにつれて光電効果の断面積は小さくなってきますから、相対的にコンプトン散乱が主になるということは起こります。
光子と物質の相互作用についてはこのぐらいにして、次はスペクトル解析の基礎についてまとめていきます。
スペクトル解析の基礎
放射線分野におけるスペクトル解析はエネルギースペクトル、すなわち各エネルギー成分の波高値を並べて表示したものを取得し、それらを解析することで物質の同定や定量を行うものです。

上図はかなり簡略化したもので、実際はもっとごちゃごちゃしたものが多いです。
全吸収ピークから核種の同定、波高値から定量が可能となります。
このようなスペクトルを得るためには、エネルギー弁別機能を備えた放射線測定器が必要になります。
そして物質の同定、定量をより正確に行う(物理現象を正確に追う)ためには放射線測定器のエネルギー分解能も重要になってきます。
このエネルギー分解能については別の機会に説明することにして、今回は先程復習した各相互作用がスペクトルにどのように現れるか見ていきましょう。
①全吸収ピーク
この全吸収ピークは放射線測定器に入射した光子エネルギーが全て吸収された場合に生じるピークです。

ここで少し注意が必要なのは、放射線測定器が見ている(検出している)のはあくまで放射線によって電離された電子の挙動です。
放射線測定器の基本原理を理解しておけばこれは大丈夫だと思いますが、少し意識して読み進めてください。
さて話を戻しますが、この全吸収ピークは先程の光電効果、コンプトン散乱、電子対生成の全てに関わるものです。
例えば、光電効果が生じた場合、入射光子のエネルギーは放出される光電子とその結合(束縛)エネルギーに分かれます。
ここも勘違いしやすいのですが、全吸収ピークは光電子の検出だけでは足りず、結合エネルギーも何らかの形で検出される必要があります。
この何らかの形というのが先程少しだけ説明した特性X線やオージェ電子です。
光電子が完全に吸収されたとしても、この特性X線などが放射線測定器から逃げてしまうと全吸収にはなりません。
このように意外と細かく物理現象を理解しておく必要があります。
コンプトン散乱、電子対生成も同様に考えられます。
コンプトン散乱の場合は散乱光子が放射線測定器から逃れることなく光電効果などを起こして検出される必要があり、電子対生成の場合は対消滅で生じた消滅放射線が2本とも検出される必要があります。
②コンプトン散乱による連続スペクトル
先程の全吸収ピークは理想的には単一のエネルギーであるため、線スペクトルとして表れていましたが、コンプトン散乱が生じ,散乱光子が放射線測定器から逃れた場合、コンプトン電子のエネルギーは散乱角によって異なるためスペクトルは連続スペクトルとなります。

この中でもコンプトン電子の最大エネルギー(コンプトンエッジ、コンプトン端)と後方散乱ピークの2つが問われる可能性があります。
まずはコンプトンエッジから見ていきます。
先程書いた通り、コンプトン電子のエネルギーは、
で求められます。
このエネルギーが最大になるとき、上式の分母が最小になる必要があります。
変化するのは散乱角のみであるため、
が最大すなわち
となります。
これを満たすは180[°]ですね!
続いて、後方散乱ピークは検出器の後方から入射してきた散乱光子によるピークです(図では省略しています)。
この場合は逆に散乱光子のエネルギーの式から、
に代入して求めることができます。
知識として「コンプトンエッジは散乱角180度の時」と覚えるのも悪くはないですが、上で使用した2式も結局覚えなければならないので、式から考えて導出するという風にしておいたら良いかと思います。
③シングルエスケープピーク、ダブルエスケープピーク
これは電子対生成のみが関係します。
全吸収ピークで説明した通り、対消滅によって生じた消滅放射線が2本とも検出されることにより電子対生成が起きた場合も全吸収ピークを生じます。
この消滅放射線が1本もしくは2本とも検出器の外に逃げ出す(エスケープ:escape)ことにより生じるピークをそれぞれシングルエスケープピーク、ダブルエスケープピークと呼びます。

この消滅放射線のエネルギーは0.511 MeVと決まっていますから、シングルエスケープピークは全吸収ピークから0.511 MeV低いエネルギーに生じ、ダブルエスケープピークは全吸収ピークから1.022 MeV低いエネルギーに生じることが分かるかと思います。
さて、かなり長々と書いてきましたがだいたい理解できたでしょうか?
やっと問題解説です笑
問題解説
前置きがなかなか長くなってしまったので、問題を再掲しておきます。
問17 NaI(Tl)γ線スペクトロメータにより、エネルギー未知のγ線の波高分布スペクトルを測定したところ、全吸収ピークが600チャネルに、コンプトンエッジが400チャネルに観測された。この場合のγ線エネルギー[keV]はいくらか。ただし、このスペクトロメータの零点調整はなされている。
1.320
2.511
3.662
4.835
5.1,170
公益財団法人原子力安全技術センター
(https://www.nustec.or.jp/syunin/syunin05.html)
より引用
まずは少し聞きなれないスペクトロメータの零点調整について補足します。
これはスペクトロメータで観測される全吸収ピークのチャネル番号が光子エネルギーと正しく比例関係にあることを示しています。
簡単な例で言うと、光子エネルギー1 MeVのγ線の全吸収ピークがチャンネル番号1000で検出された場合、チャネル番号500では0.5 MeVの波高値を示すといったような感じです。
補足を終えたところで、問題を解いていきましょう。

上図は理想的なスペクトルであり、実際はNaI(Tl)γ線スペクトロメータなのでもう少しぼけた以下の図のような感じかもしれません。

先程の補足通り、全吸収ピークの600チャネルはγ線の光子エネルギーを示します。
また、コンプトン電子のエネルギーは
を用いて、
と表され、コンプトンエッジは = 180[°]の時生じるため、
となります。
補足で確認した光子エネルギーとチャネル番号の比例関係から、以下の関係が成り立つことが分かります。
式を少し整えると、
= 511 keVであるため、このγ線エネルギーは511 keVであると分かります。
γ線エネルギーが1.022 MeV以下なので、電子対生成が生じず、シングルエスケープピークやダブルエスケープピークは生じまていませんね。
問題自体は大したことないのですが、スペクトル解析のイメージがつかめていないと少しわかりにくかったかと思います。
放射線取扱主任者の試験ではこういった問題の解説を読んで理解するだけで満足するのではなく、その背景となる知識などを少しずつ蓄えていくことが重要になります。
この過程にきちんと取り組むかどうかによって、記憶の定着度合いも変わってくると思います。
せっかく勉強するのだから、国試(放射線技術系の人のみ)のためにもしっかり理解できるといいですね!
ではまた!
主任者試験を極める①(H29 第1種放射線取扱主任者試験 物理学 問28)
こんにちは!
今回は第1種放射線取扱主任者(以下、主任者)試験の少し難しいと思った問題について、基礎事項を確認しながらまとめていきます。
全何回になるかは特に決めていませんが、不定期に更新していきたいと思っています。
主任者試験の問題は診療放射線技師国家試験の問題よりも理解が難しい問題が多いかと思います。
難しい問題を解けないと合格できないかと言われるとそんなことは無いんですが、今年(2020年度)の試験は延期されたことですし、せっかく勉強するなら理解してしまった方が良いですよね。
暗記事項もたくさんありますが、これについては参考書などを見たほうがキレイにまとめられていると思うので、基本的に計算を含む少しややこしめの問題を対象としていきます。
そのため必然的に科目は物理学、計測学に偏ると思われます。
多くの人がつまづく部分なので、「この問題参考書の解説読んでも意味わからない💢」と思ったら、このシリーズを参考にしてもらえればと思います。
では早速、今回は平成29年度物理学問28を扱っていきます!
問28 GM計数管の入射窓の前方に線源Aを置いて1,000秒間計数したところ、100,000カウントであった。次に線源Aの横に線源Bを置き計数したところ、1,000秒間で197,000カウントを得た。最後に線源Aを取り去り、同じく1,000秒間計数したところ、計数値は100,000カウントであった。バックグラウンド計数率は0.5cpsである。このGM計数装置の分解時間[μs]はいくらか。
1.100
2.130
3.160
4.190
5.220
公益財団法人原子力安全技術センター
(https://www.nustec.or.jp/syunin/syunin05.html)
より引用
いきなりなかなか重たそうな問題ですね。
では、基礎事項の確認から始めていきます。
基礎の確認
今回の問題はGM計数管の計数率に関する問題です。
放射線計測学をあまり知らない人が読むと「なぜこんなことが起きるの⁇」と思ってしまうかもしれません。
線源A単独と線源B単独で計測した時の合計よりも線源A+線源Bで計測した時の方がカウントが少なくなってしまっているからですね。
先に言ってしまうと、これは検出器の数え落としによって起こる現象です。
まずはGM計数管の原理から簡単に確認しましょう。
GM計数管の原理
GM計数管は以下のような構造をしています。

図を見てわかるように計数管内に放射線が入射すると、ガスを電離しイオン対(電子と陽イオン)が生じます。
計数管の陽極と陰極には高電圧がかけられており、電子は陽極に向かって加速されます。
GM領域の高電圧では一つの電子イオン対でも電子なだれを起こすため、電離量に関係なく大きな波高値を生じます。
また、この電離(電子なだれ)により生じた陽イオンも電場の向きに従って陰極へ加速されますが、電子に比べて重いイオンは速度が遅いため、陽極の周りに停滞し陽イオンの筒のようなものを作ります。

これにより電圧が降下するため、放射線の入射による1次電離が生じても検出器は応答しません。
この応答がない(小さい)時間(不感時間、分解時間、回復時間)について続いて見ていきましょう。
不感時間、分解時間、回復時間とは
前述したように、放電直後の陽イオンの筒の影響で電圧が降下し、放射線が入射し1次電離を生じても検出器が応答しない時間があります。
これが不感時間と呼ばれるものです。
不感時間に加えて、電圧が回復し波高弁別レベルを超える出力波高が生じるまでの時間を分解時間と呼ばれます。
この時点の出力波高はパルスとして認識されるギリギリの大きさであり、さらに十分に時間が経過することで最初のパルスの波高値まで戻るまでの時間は回復時間と呼ばれます。
図で示すと以下のようになります。

印加電圧や波高弁別レベル、計数管の形状にも影響されますが、GM計数管の分解時間は数百μs程度です。
先程も書いたように、この分解時間内では放射線が入射して1次電離を生じても検出器は計数することができません。
この時間内に生じた放射線(電離)は「数え落とされる」というわけです。
数え落とし
検出器の数え落としについて真の計数率を[cps]、測定計数率を
[cps]、分解時間を
[s]とすると以下のような関係式が成り立ちます。
左辺は真の計数率から測定計数率を引いたものなのでそのまま1秒当たりの数え落としを示します。
右辺は少々ややこしいので説明します。
分解時間[s]は実際にGM計数管で計数されるたびに生じるものです。
つまり測定計数率[cps]と分解時間
[s]の積
はその検出器の1秒当たりの検出不能時間を示します。
これは真の計数率のうち検出不能となる割合とみることもできます。
このため、真の計数率[cps]に
を乗じることで1秒当たりの数え落としが求められるというわけです。
これで式の意味が理解できたでしょうか?
これが理解できていれば、先程の式を変形しただけの
とか
といった式を覚える必要はなくなります。
基礎の確認はこの程度で大丈夫です。
これで恐らく問題文の意味が分からないということは無いでしょう。
では、問題を解いていきます!
問題の解説
いきなり計算を始めるのではなく、まずは文字を設定して考えていきます。

先程確認した関係より、各条件の真の計数率はそれぞれ、

と書けます。
また、真の計数率についてバックグラウンドの真の計数率をとすると以下の関係が成り立ちます。

バックグラウンドの計数率は小さく、分解時間の影響を無視できるため、測定計数率は
と考えられます。
(1)~(4)式より、

このまま計算しても解けないので、少し近似を行います。
のとき、
の近似が成り立ちます。
なぜこの近似が成り立つのか気になる方は以下の補足を読んでください。
基本は飛ばしてかまいません。
ーーーーーーーーーーーーーーーーーーーーー
<補足>マクローリン展開による近似
としてマクローリン展開すると
となります。
第2項もしくは第3項あたりまでで近似すれば十分であり、今回は第2項までで近似しています。
ーーーーーーーーーーーーーーーーーーーーー
このため、(5)式は

と表せます。少し整理すると、

となり、分解時間が求められます。
この分解時間を求める方法は2線源法と呼ばれます。
後は問題文から代入するだけですね。
題意より
[cps]
[cps]
[cps]
であるため、分解時間[s]は、
[µs]
と求まります。
2線源法の計算は近似などを含んでおり、なかなか難しかったかと思います。
実際問題を解くことを考えると最後の分解時間を求める式を覚えておくのが手っ取り早いと思いますが、かなりゴチャゴチャした式なので導出も理解しておくと良いかもしれません。
ひょっとすると物理の多肢択一式(旧物化生の問題)で導出の出題があるかもしれませんね。
今回の問題のように初見では歯が立たなそうな問題も一度理解しておくと解ける可能性が高くなると思います。
診療放射線技師の国家試験ではおそらく2線源法の計算までは出題されないと思いますが、真の計数率の式は頻出なのできっちり理解しておくと良いです。
何か誤りがあれば教えてください。
ではまた!
Dual energy CT入門④
こんにちは!
今回でDual energy CT入門は最後になります。
最後はDual energy CTの臨床応用について書いていきます。
臨床応用といっても、私自身が臨床で実際に見た物ではなく、単に書籍などから仕入れた情報なのであくまでも参考までにお願いします。
さて、多くの書籍では部位ごとにこれに使える、あれに使えると書かれていますが、今回は部位ごとではなくもう少し大まかな用途を書いていきます。
細かい用途はたくさんありますが、大きく分けて4つの用途があります。
1.造影効果の向上
2.被ばく線量の低減(造影)
3.物質弁別
4.アーチファクト低減
第1回でも簡単には書きましたが、それぞれの項目について少し詳しく書いていきます。
1.造影効果の向上
造影効果の向上は以下の2パターンが考えられます。
①仮想単色X線画像の低keV画像
②ヨードマップ
それぞれ見ていきましょう。
①仮想単色X線画像の低keV画像
仮想単色X線画像については前回までの記事である程度書いてあるのでここでは省略します。
まだ読んでいない人はぜひ一度読んでみてください。
yuruyurudokugaku.hatenablog.jp
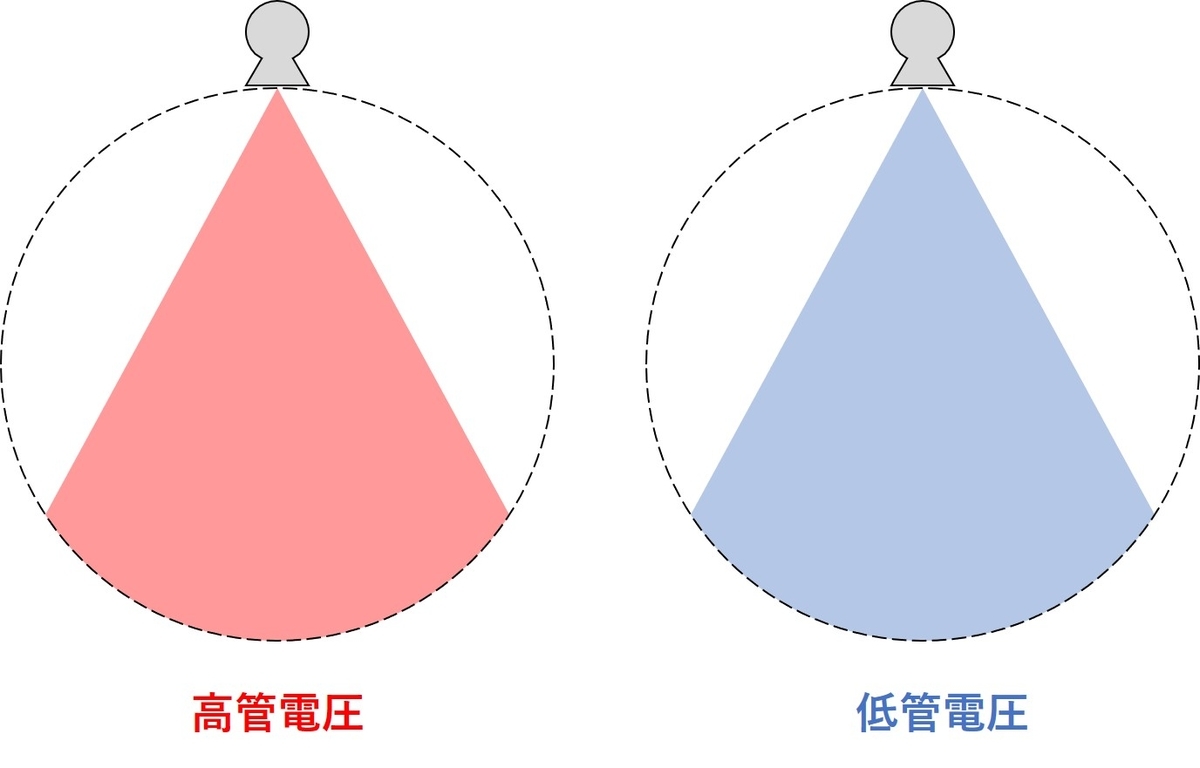
この仮想単色X線画像を用いて造影効果を高めるためには低keV画像が用いられます。
一般撮影などでもコントラストをつけたいときには低管電圧で撮影を行いますよね。
管電圧が低い領域では物質の減弱係数の差が大きくなる場合が多いため、低管電圧の撮影が用いられます。
ヨードの造影効果上昇は少し違うという意見も見かけましたが、基本的には同じように考えていいと思います。
おそらく画像全体のコントラストが向上することと、造影剤(ヨード)と軟組織のコントラストが向上することを分けて考えているということだとは思うのですが(違っていたらぜひ教えてください)。
以下に骨、軟組織(水)、ヨードそれぞれの質量減弱係数のエネルギー依存性を示します。

この図を見れば低管電圧でコントラストが向上することが想像できると思います。
これによりより細かい血管が見えたり、腫瘍などがより明確に見えたり、造影剤を減量できたりするわけです。
innavi net 画像とITの医療情報ポータルサイト
(https://www.innervision.co.jp/sp/ad/suite/canonmedical/sup201905/session2-1_ct1)
より引用
これに頼りすぎるのは良くないのかもしれませんが、血管系の造影でタイミングがうまく合わず、造影不足になった場合のリカバリーも効きそうですよね。
これが実用レベルになればなかなか有用な気がします。
②ヨードマップ
このヨードマップはどちらかというと物質弁別に含まれるのですが、これも造影効果を向上させるという意味では有効と考えられます。
簡潔にいうとヨードマップはその名の通り、ヨードの分布を示すものです。
カラースケールでヨードの量を示すアプリケーションもあり、より定量性の高い解析が可能になるようです。
他の高吸収物質との区別もつきやすくなります。
2.被ばく線量の低減(造影)
この被ばく線量の低減は造影を含む検査にのみ適応できるものです。
どういうことかというと、これまた物質弁別をうまく使用することで仮想非造影画像を作成可能になるということです。
造影検査を行う際、多くの場合造影前と造影後の2回の撮影が必要になります。
しかし、造影画像からヨードを除いた仮想的な非造影画像が作り出せるのであれば撮影が一回で済むというわけです。
(http://rad.med.keio.ac.jp/dx/study/cont07/)
より引用
ただこの仮想非造影画像はあくまで仮想的なものであり、本来の非造影画像と全く同じように扱えるわけではありません。
どこまで使えるのかは分かりませんが、症例によっては被ばく線量の低減に十分寄与できるような気がします!
3.物質弁別
この物質弁別ですが、先ほどまで見てきたように様々な使われ方をするようです。
例えば、
・ヨードと他の物質(石灰化、骨など)の弁別→ヨード密度画像、ヨードマップなど
・胆石、腎石、尿路結石などの主成分の解析→実効原子番号解析など
・肝臓の脂肪量の定量→脂肪密度画像など
と多様です。
CTではなかなか難しかった物質の弁別により、MRIでしか出来なかった検査の代替が可能となる部分もあるようです。
ただMRIと違い、結果的に被ばくを伴うことになるので、その目的のみでの検査というのは難しいかもしれないですね(撮影時間的にはCT に軍配が上がる場合もあるかもしれませんが)。
この物質弁別はまだまだたくさんの用途が考えられており、とても面白そうですね。
4.アーチファクトの低減
第1回の記事でも少し書きましたが、仮想単色X線画像を用いることで、ビームハードニングアーチファクト、ひいては金属アーチファクトの補正が可能となります。
この仕組みは各社それぞれで異なることと、入門にしては少しややこしく記事が長くなってしまうので少し省略しながら説明していきます。
ビームハードニングはCTで使用するX線が連続スペクトルを持つ連続X線であるために生じます。
投影方向や高吸収の構造物などによって画像再構成時に矛盾が生じアーチファクトを発生するというわけです。
これはDual energy撮影における高管電圧・低管電圧撮影においても同じです。

上式は2つの基準物質(水とヨード)を仮定した式であり、高管電圧撮影と低管電圧撮影それぞれの投影データを示しています。
それぞれのエネルギーが単一であれば質量減弱係数も一意に定まるため問題は生じないのですが、連続エネルギーの場合、質量減弱係数はX線のパス上で一定になりません。
となると、それぞれの厚み、すなわちその量や密度の正確性も低下していることが考えられます。
これらの影響をできるだけ抑えるために、各管電圧撮影におけるエネルギー(実効エネルギーのようなもの?)と各物質の厚さ(量、密度)を未知数とした最小化問題を解くことで解(より正確な値)を求めることになります。
式で示すと以下の通りです。

意味が全く分からないという方は読み飛ばしてもらって構いませんが、この最小化問題を解くことで高管電圧と低管電圧それぞれの実効エネルギー(一意に定まる)と各物質の量が正確に定められることになります。
これによりDual energy解析の結果がより正確になるため、仮想単色X線画像でビームハードニングを補正した通常の120kVp画像に近いものを得ることができるという流れのようです。
また、根拠はいまいち理解できていないのですが、高keV画像において金属アーチファクトを低減することが可能なようです。
私も理解があいまいなので全然違う!というところがあったら是非教えてください!
最後に少し内容が重くなってしまいましたが、だいたいこのような臨床応用があるようです。
国試にはまだ出題がないので、今後出題されるとしてもこの程度押さえておけば十分だと思います。
Dual energy CT入門という記事を書いていながら、私もかなり入門中なので今後も勉強していきたいと思います。
ではまた!
Dual energy CT入門③
こんにちは!
第3回ではDECTの撮影方式についてまとめていきます。
授業などでは原理よりむしろこの撮影方式だけを習うという場合が多いのではないでしょうか。
とりあえず撮影方式の種類は覚えていても、それぞれのメリット・デメリットを理解しているという方は少ないと思うので、各方式について確認していきます!
DECTの撮影方式
まずはDECTの各撮影方式について確認していきます。
DECTの撮影方式には、
1.連続2回転(Sequential scan)方式
2.2管球(Dual X-ray source)方式
3.高速スイッチング(Rapid kV switching)方式
4.2層検出器(Dual-layer detector)方式
5.分割(Sprit filter)方式
などがあります。
他にもあるかもしれませんが、この5つを理解していれば大方大丈夫だと思います。
では、各方式の概要とメリット・デメリットについてみていきましょう。
1.連続2回転(Sequential scan)方式
これは同一箇所に対して管電圧を切り替えて連続的に2回転することで2つの異なるエネルギーで撮影した画像を得るという方式です。
非常に単純な原理ですね。図で示すと以下のようになります。
では、メリット・デメリットを確認しましょう。
<メリット>
・エネルギー分離が良い
これは前回の記事で説明したエネルギーセパレーションが良いということですね。より正確なDual energy解析が可能となります。
方法としては低管電圧はそのまま、高管電圧は錫(Sn)フィルタなどにより低エネルギー成分を除くなどがあります。
・管電圧・管電流を完全に独立制御可能
低管電圧撮影と高管電圧撮影が別々に行われるため、それぞれの管電流なども独立制御となり、より最適な条件での撮影が可能となります。
・投影データ上でのDual energy解析が可能
管球、被写体、検出器の位置関係が低・高管電圧で同じであれば投影データでのDual energy解析が可能となります。
しかし、次のデメリットから必ずしも可能とは言えないかもしれません。
<デメリット>
・時間差が生じる
連続2回転とはいえ、やはり時間差が生じてしまいます。
この間に被写体が動いてしまうと正確な解析ができなくなる可能性があります。
・被ばく線量の増加
これは少し微妙な問題ですが、2回撮影を行うため被ばく線量が増加することが考えられます。
2.2管球(Dual X-ray source)方式
2管球方式はその名前の通り、CT装置のガントリ内にX線管球が2つ内蔵された方式です。
2つの管球は90度位相がズレた位置にあり、それぞれ高管電圧と低管電圧でX線を放出します。
図で示すと、以下のようになります。

では、メリット・デメリットを確認しましょう。
<メリット>
・エネルギー分離が高い
・管電圧・管電流を独立制御可能
これらは先ほどの連続2回転方式と同じですね。
・(連続2回転方式に比べて)撮影時間が短い
これは同じメリットを有する連続2回転方式と比べて撮影時間が短いという意味です。
他の方式に比較して撮影時間が短いというわけではありません。
<デメリット>
・投影データ上でのDual energy解析が不可能
2つの管球でスキャン軌跡に約90度の位相差があり、2つの投影データは一致しません。
このため、この方式を採用している場合、Dual energy解析は投影データベースではなく画像ベースとなります。
・散乱線によるアーチファクト
エネルギー分布の異なるX線が90度の位相差をもって同時に照射されるため、互いの系がそれぞれ散乱線源になってしまいます。
クロス散乱線と呼ばれるものです。
・ハードウェアのコストが高い
X線管、検出器が2組必要となるため、もちろん既存のCTには使用できませんし、CT装置自体の価格も他の方式より高くなる場合が多いようです。
・撮影FOVが小さい
ガントリ内に2つの撮影系を設置するため、スペース上の問題が生じ、FOVに制限がかかっていましたが、現在はほぼ解消されているようです。
3.高速スイッチング(Rapid kV switching)方式
高速スイッチング方式では管電圧を数ms以下の短い間隔で切り替えながら連続的に撮像することで、ほぼ同時に2つの異なる電圧で撮像したようなデータを取得することが可能となります。
図で示すと以下のようになります。

では、メリット・デメリットを確認しましょう。
<メリット>
・ハードウェアのコストを比較的低く抑えられる
管球と検出器は1組でよいので、2管球方式よりはコストを低く抑えられる場合が多いです。
・投影データ上でのDual energy解析が可能
厳密にはスイッチング間隔のずれが生じますが、ほぼ同じ軌跡を通るため投影データを用いた解析が可能となります。
何らかの補間処理が行われているものもあるようです。
<デメリット>
・管電圧の安定性が低い(エネルギー分離が悪い)
高速での切換を行うため、電圧の安定していない過渡期の割合が大きくなります。

これにより実効管電圧が不確かになり、エネルギーセパレーションが悪くなってしまいます。
かといって、スイッチング間隔を長くすると投影データのギャップが大きくなり、投影データベースのDual energy解析が難しくなってしまいます。
・管電流の変調が困難
ここでいう管電流の変調は主に高管電圧-低管電圧間の変調です。
基本的に低管電圧では線量(mAs)を多くする必要があるため、高管電圧より収集時間を長めにとってスイッチングを行うことで対応されているようです。
また、同じ高速スイッチング方式であっても管電圧の安定性や管電流変調を重視したものもあり、そちらでは投影データ間のギャップが大きくなってしまいます。
このギャップの補間不足は今流行りのディープラーニングなんかで補われるのでしょうか。
4.2層検出器(Dual-layer detector)方式
2層検出器方式では用いるX線源は単一ですが、低エネルギー用と高エネルギー用の2層の検出器を用いることで同時に2つのエネルギーでCT撮像を行います。
図で示すと以下のようになります。

1層目は低エネルギー成分、2層目は高エネルギー成分に適したシンチレータを用いた検出器になっています。
では、メリット・デメリットを確認しましょう。
<メリット>
・2つのエネルギー画像を空間的・時間的に完全に一致した条件で撮像可能
2層の検出器は同位置に設置されているため、空間的・時間的に一致していることは明らかです。
・投影データ上でのDual energy解析が可能
上の特徴から考えられるように完全に同じ物理現象から得られる投影データであるため、真の意味で投影データベースのDual energy解析が可能となります。
<デメリット>
・エネルギー分離が悪い
一応2層の検出器で低エネルギー成分・高エネルギー成分をそれぞれ分離しているというものの、元のX線は単一のX線源から放出されているものであるため、完全な分離は難しいと考えられるでしょう。
・検出器のコストが高い
検出器が2層ですからコストは高くなりそうですよね。
・管電流の独立制御ができない
これも高管電圧-低管電圧間での管電流の変調です。
・受光線量効率が低い
これは検出器の構造上避けられないものです。
一般的な検出器はシンチレータの直下にホトダイオードが設置されています。

しかし、2層検出器の場合、1層目の直下にホトダイオードを設置することはできません。
このため、1層目と2層目の各シンチレータの横にホトダイオードを配置するような構造となります。

これにより検出器の隔壁が厚くなり、不感部分が増えるため、受光線量効率が低下してしまいます。
5.分割(Split filter方式)
この方式では単一のX線管から発生したX線を特殊なフィルタを用いることで、低エネルギー成分・高エネルギー成分を頭尾方向に分割し、同時に2つのエネルギーで撮像します。
図で示すと以下のようになります。

では、メリット・デメリットを確認しましょう。
<メリット>
・ハードウェアのコストを抑えられる
これは基本的にフィルタを変えるだけで実現可能なため、従来のCT装置でも使用可能だそうです。
検出器側の処理はどうなっているのでしょう?よくわかりません笑
<デメリット>
・エネルギー分離が悪い
フィルタでエネルギー成分を分割しているだけなのでやはりエネルギーセパレーションはあまりよくありません。
・投影データ上でのDual energy解析はできない
頭尾方向に分割するため、スキャン軌跡が頭尾方向にわずかにずれてしまいます。
このため、投影データにもずれが生じ投影データベースのDual energy解析はできません。
・管電流は独立制御できない
2層検出器方式と同じです。
まとめ
ここまで説明してきたように、Dual energy CTには様々な撮影方式があり、それぞれにメリット・デメリットがあります。
また、各社各装置はそれぞれのデメリットを克服するために工夫を凝らしていることでしょう(なぜか偉そう笑)。
今後どのように開発が進んでいくのでしょうか。
楽しみですね。
次回は臨床応用について書いてみたいと思います。
ではまた!



