2020-04-21

Dual energy CT入門②

CT 放射線物理学独学

こんにちは！

第2回ではDECTの簡単な原理についてまとめていきます。

DECTの原理といっても、実は各社各装置のアプリケーションによって仕組みや目的が異なっている場合があるので、全てが今回説明する原理に基づくとは限りません。

投影データベースなのか画像ベースなのか、撮影方式はどれかなどによっても異なります。

といった理由もあり、今回紹介するのは基本的な原理になります。

では、基本の物理から確認していきましょう！

DECTの物理
- 光子と物質の相互作用
- Dual Energyの意味
仮想単色X線画像の作成
DECTの課題

DECTの物理

光子と物質の相互作用

この記事を読んでくれている方にとっては退屈かもしれませんが、一応光子と物質の相互作用について復習しておきます。

光子と物質の相互作用には弾性散乱、光電吸収、コンプトン散乱、電子対生成、光核反応があります。

線減弱係数はこれらの相互作用それぞれの減弱係数の和となります。

診断領域で用いられるX線のエネルギーでは特に光電吸収とコンプトン散乱が主となります。

したがって、CT撮影によって得られる線減弱係数は光電吸収とコンプトン散乱の線減弱係数の和となります。

式で示すとこんな感じですね。

　 $\mu = \mu_p + \mu_c$

光電効果とコンプトン散乱の2つの相互作用はどちらも光子のエネルギーに依存して変化しますよね。

このため、先程の式は、

　 $\mu(E) = \mu_p(E) + \mu_c(E)$

と書けます。

これで完成と言いたいところですが、まだ考慮しなければならないものがあります。

線減弱係数、正確に言うと質量減弱係数は物質によって異なるものでしたよね。

X線のエネルギーが同じであっても、光電効果が多くを占める物質とコンプトン散乱が多くを占める物質があります。

f:id:Yuru-yuru:20200420222918j:plain:w400

つまり、物質の質量減弱係数は物質（原子番号）に依存するファクタと物質に依存しないエネルギーの関数に分けることができると考えられます。

これはすなわち、各物質の質量減弱係数が光電効果とコンプトン散乱のエネルギー関数の線形荷重和で表せるということです。

何かとても難しいことを言っているように見えるかもしれませんが、式で表すと以下のような簡単な式で表せます。

　 $\mu(E) = \alpha f_p(E) + \beta f_c(E)$

　 $f_p(E)$ ：光電効果のエネルギー関数

　 $f_c(E)$ ：コンプトン散乱のエネルギー関数

　 $\alpha$ 、 $\beta$ ：物質固有の荷重係数

この光電効果とコンプトン散乱のエネルギー関数（この言葉があっているのかは微妙ですが）がそれぞれヨードと水など2つの基準物質の質量減弱係数として考える場合も多々あります。

これは診断領域のエネルギーではヨードの相互作用がほぼ光電効果、水の相互作用がほぼコンプトン散乱に近似できるからです。

DECTのアプリケーションではむしろ2つの基準物質によるものの方が主流ですが、個人的には上記の考え方の方が原理に忠実だと思ったので今回はこの考え方でいきます！

Dual Energyの意味

先程の式を眺めてみると、左辺の $\mu (E)$ は撮影によって得られる値であり、右辺の光電効果・コンプトン散乱のエネルギー関数は既知のものであるため、分からないのは物質固有のパラメータである $\alpha$ 、 $\beta$ です。

以前少し書いたように、仮想単色X線画像を作成するためには各物質のCT値（線減弱係数）がエネルギーの変化に対してどのように変化するかが分からなければいけません。

ではこの $\alpha$ 、 $\beta$ を求める方法について考えてみましょう。

まず、任意のエネルギーE（実際には実効エネルギー）で撮影した画像から $\mu(E)$ が得られます。

さらに、光電効果・コンプトン散乱それぞれのエネルギー関数もエネルギーを決めれば一意に定まるため、定数と考えられます。

こうした場合、先程の式は $\alpha$ 、 $\beta$ を未知数とする二元一次方程式と考えられます。

たとえば、このような式と同じように考えられます。

　 f:id:Yuru-yuru:20200420220211j:plain:w150

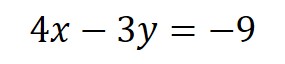
これを解きたいところですが、未知数が2つあるのに方程式は1つしかありません。

これが解けないことは中学で数学をやっていればわかるはずです。

では、どうすればよいか。

そうですね。同じxとyが満たす式をもう一つ探すしかありません。

　 f:id:Yuru-yuru:20200420215936j:plain:w150

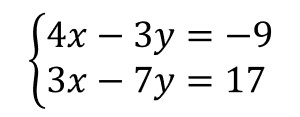
こうなればただの連立方程式になり、解くことができると思います。

ではCTではどうすればいいか。

もうピンときている方もいると思いますが、異なるエネルギーで撮影すればよいということになりますね！

低い方のエネルギーを $E_1$ 、高い方のエネルギーを $E_2$ とすると、

　 $\mu (E_1) = \alpha \mu_p (E_1) + \beta \mu_c(E_1)$

　 $\mu (E_2) = \alpha \mu_p (E_2) + \beta \mu_c(E_2)$

これは先ほどの連立方程式を解くのと同じ計算を行えばよいことになります。

ここが2つの異なるエネルギーで撮影する意味になります。

理想を言えばもっとたくさんのエネルギーで撮影すればいいと思うかもしれませんが、そんなことをする意義も時間もありません。

2つで十分ということです。

これにより物質固有のパラメータ $\alpha$ 、 $\beta$ が求められました。

では最後に仮想単色X線画像の作成について見ていきます。

仮想単色X線画像の作成

ここまで読んで大方理解できていれば、もう説明はいらないかもしれませんが一応説明していきます。

先程の計算で物質固有のパラメータ $\alpha$ 、 $\beta$ を求めることができました。

となれば、あとは仮想単色X線画像を作成したい任意のエネルギーで撮影したときの $\mu (E)$ を求めることになります。

簡単ですね。

光電効果・コンプトン効果それぞれのエネルギー関数にそのエネルギーを代入してやれば任意のエネルギーにおける $\mu (E)$ が求まるというわけです。

この過程を画像のピクセルごとに行っていけば仮想単色X線画像が作成できることは想像に難くないと思います。

かなり単純化しましたが、基本的にはこのような原理で仮想単色X線画像が作成できます。

ただ、これはかなり理相的な話であって、もう少し考えなければならないことがあります。

DECTの課題

DECTの課題はまぁたくさんあると思いますが、今回はエネルギーセパレーションについてだけすこし説明します。

知っての通り、CT撮影に用いるX線は単一エネルギーではなく連続エネルギーを持つ連続X線です。

先程まで説明してきた原理で使用する2つの異なるエネルギーはどちらも実効エネルギーになります。

なんとなくのイメージで十分ですが、エネルギー成分の重複を少なくするため、使用する2つの異なるエネルギーはできる限り離れていることが望ましいです。

f:id:Yuru-yuru:20200420224227j:plain:w500

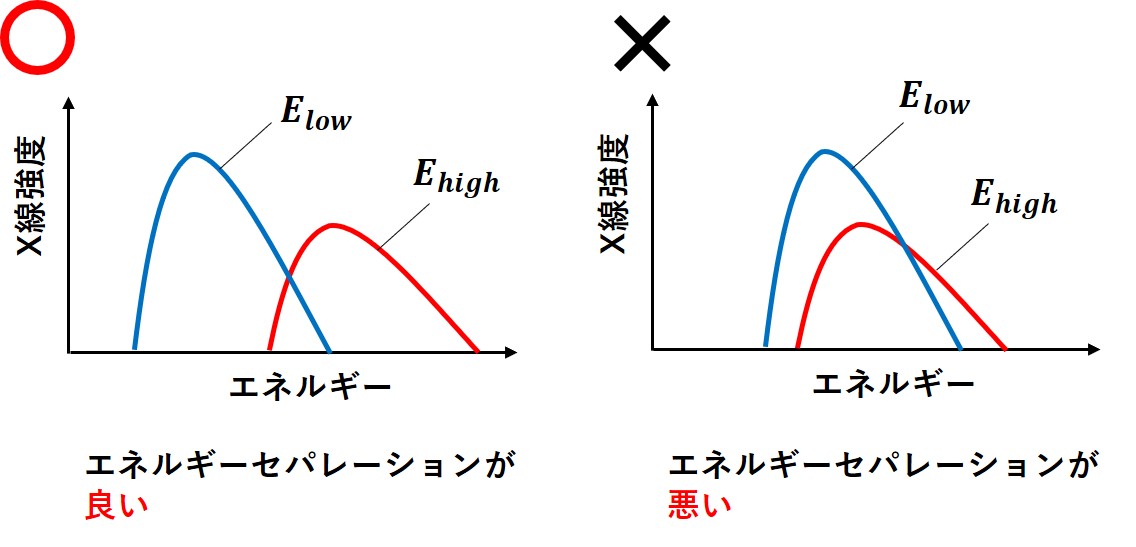
これがエネルギーセパレーションが良いということです。

普通に管電圧を変えただけでは重複しているエネルギー成分が多く、エネルギーセパレーションが悪い場合が多いので、フィルタを使ったり、検出器を変えたりなどいろいろな工夫がされているようです。

何となくDECTの原理が理解できたでしょうか？

次回はDECTの撮影方式についてまとめていきます。

何か誤りがありましたら教えてください。

ではまた！

2020-04-18

Dual energy CT入門①

CT 放射線物理学独学

こんにちは！

今回から4回に分けてDual-energy CTについてまとめていきたいと思います。

DECTは現在CTにおける重要な研究テーマの一つですが、学部の授業などで細かい所まで触れることは少ないかと思います。

ですが、国試の出題にもDECTを意識しているのかなという問題もあり、今後標準的に学ぶ内容になっていくかもしれません。

まだ開拓中の技術ですから、書籍によって書いてあることが異なることも多々あるので、あくまで私が勉強した内容のまとめであることを理解したうえで読んでください。

第1回ではまず「DECTが何に使われるか」について書いていきます。

私自身の考えですが、「何のために使われるのか、何に必要なのか」を分かっているのと分かっていないのでは勉強のモチベーションがかなり違います！

いくつか馴染みのない用語も出てきますが、とりあえずスルーして「こんなことができるんだー」ぐらいの気持ちで読んでいただければと思います。

では、早速みていきましょう！

DECTとは？

そもそもDECTがどのようなものか何となくでも分かっていないと用途を説明しても「？？？」だと思うので、簡単にまとめます。

Dual-energy CT（デュアルエナジーCT）という名前から2つの異なるエネルギーのX線を使用するCTなんだろうな、ということは想像できると思います。

2つの異なるエネルギーのX線を使用した技術として骨密度測定のDXA法やDES（デュアルエナジーサブトラクション）など、国試にも出題されるものもいくつかありますよね。

一般撮影では通常の撮影であっても撮影部位によって管電圧を調整しますが、CTでは基本的に120kVp程度の管電圧が使用されることが多いです。

DECTは120kVpより低い管電圧と高い管電圧のX線で撮影を行い、得られたデータから通常のCT撮影では得られない情報を得ようとするものです。

2つの異なる管電圧での撮影を行う方式としてはdual-source方式、rapid kV switching方式やdual-layer方式などがあります。

f:id:Yuru-yuru:20200418150224j:plain:w500

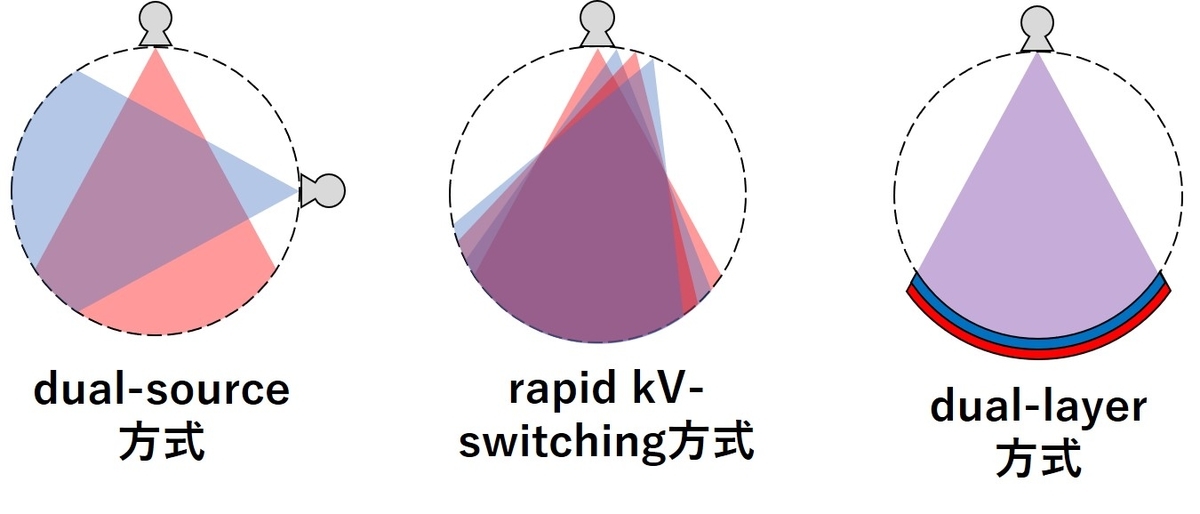
（これらの方式については第3回で詳しくまとめる予定です。）

では、低管電圧と高管電圧の撮影によって得られたデータからどういったことが可能となるのでしょうか。

DECTで可能になること

DECTで可能となることとして、大きく以下の3つが挙げられます。

　1．物質弁別

　2．仮想単色X線画像

　3．ビームハードニング補正

各項目についてもう少し詳しく見ていきましょう。

1．物質弁別

いきなり少し復習になるのですが、通常のCT撮影で得られるCT値とはどのようなものか、覚えているでしょうか？

CT値は以下のように定義されています。

　 $CT value = {\frac{\mu_t - \mu_w}{\mu_w}} \times 1000$

　μt：組織の線減弱係数

　μw：水の線減弱係数

式からも分かるように水の線減弱係数を基準に決まる値でした。

今重要なのはCT値が線減弱係数の分布を示しているということです。

線減弱係数μはこのように表せます。

　 $\mu = {\frac{\mu}{\rho}} \times \rho$

　μ/ρ：質量減弱係数

　ρ：物質の密度

この式からも分かるように線減弱係数μはその物質の原子番号に依存する質量減弱係数と物質の密度の積です。

つまり、原子番号が高く密度が小さい物質と原子番号が低く密度が高い物質では同じ線減弱係数を示す可能性があるということです！

わかりやすい例としては石灰化とヨードなどがあります。

どちらもCT画像上では高吸収（白）な物質として描出されます。

石灰化は原子番号はそこまで高くありませんが、固体であるため密度は高くなっています。

これに対してヨード造影剤は原子番号は高いものの、希釈されているため密度はそこまで高くありません。

これらが同じような線減弱係数を示す場合、2物質を区別することができません。

これは造影CT（CTA）を行う場合に問題になりそうですよね。

ここでもう一つ復習です。

質量減弱係数はX線のエネルギーによって変化するものでした。

そしてその変化は物質によって異なるものでしたよね。

細かい原理は省略しますが、DECTではこれを利用して物質の弁別がある程度可能となります。

f:id:Yuru-yuru:20200418004511j:plain:w500

「ヨードだけの画像などが見れたらいいなー」ということです。

何となく理解できたでしょうか？

では、続いて仮想単色X線画像について見ていきましょう。

仮想単色X線画像

仮想単色X線画像とは2つの異なる管電圧による撮影で得られたデータから、任意のエネルギーで撮影した画像を仮想的に生成する技術です。

2種類のエネルギー（正確には2種類の管電圧）の撮影で任意のエネルギー画像が得られるのはすごいですよね！

この任意のエネルギーはもちろんどんなエネルギーでも可能という訳ではありませんが、撮影に用いたX線の実効エネルギーより低いエネルギーや高いエネルギーの画像も作ることができます。

これを理解するためにはDECTの原理に触れる必要があるので、次回以降に詳しく説明しますが、今回はとりあえず上記の内容が可能であると考えてください。

任意のエネルギーのX線で撮影した（されたような）画像はどのような場合に役立つでしょうか？

例えば、低エネルギー画像（低keV画像）ではコントラストを増強することができます。

これは一般撮影でも言えることですよね。

このコントラスト増強は造影検査で特に役に立ちます。

造影剤と組織のコントラストが大きくなるため、造影剤の減量が可能となり、副作用の低減に有用となる可能性があります。

高keV画像においても原理は曖昧ですが、金属アーチファクトが低減される効果があるようです。

あくまで仮想的なものですが、様々なエネルギーの画像を生成できることは有用性がありそうですね。

では、最後にビームハードニング補正を見ていきます。

ビームハードニング補正

CTに限らずですが、我々が使用するX線は連続スペクトルを持つ連続（多色）X線です。

様々なエネルギーのX線が混ざっているということですね。

この連続X線が被写体に入射すると、その経路の中で低エネルギーのX線から吸収されていきます。

これによりX線のスペクトルは変化し実効エネルギーが高くなります。

これがビームハードニング（線質硬化）です。

f:id:Yuru-yuru:20200418004418j:plain:w300

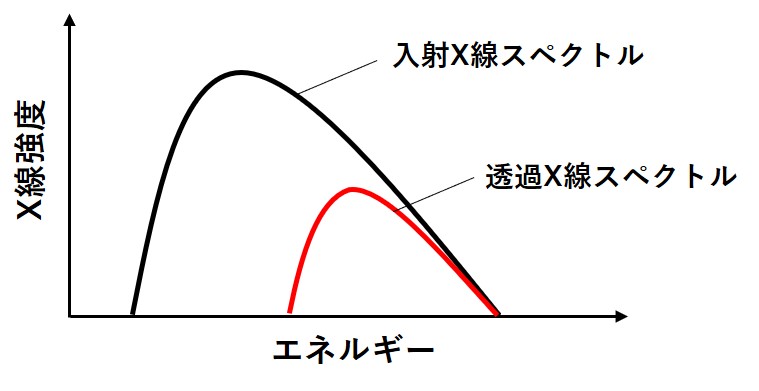
CTでは撮影方向によってこのビームハードニングの度合いが異なるため、再構成時に矛盾が生じてCT値が低くなったり高くなったりします。

カッピングやキャッピング、ダークバンドなどのアーチファクトの原因となるものです。

このビームハードニングの補正にもDECTの有用性が認められています。

DECTによるビームハードニング補正は仮想単色X線画像におけるビームハードニングを補正するものです。

言い方を変えれば、より正確な仮想単色X線画像を得るための処理です。

単色X線であればビームハードニングはないはずということです。

これもまた詳細な原理は省略しますが、異なる管電圧の撮影で得られたデータから最も尤もらしいエネルギーと透過長（量）を導く最適化問題になります。

結果的にはいかにも単色X線で撮影したような画像を作り出すことになります。

まだまだDECTが役に立つ場面はあると思いますが、これらを何となく知っているだけでその辺の学生よりかは詳しいと思います笑

次回はこのDECTの原理についてまとめていきます。

少し難しくなるかもしれませんが、ぜひ読んでください。

ではまた！

2020-04-13

「超音波ドプラ法」を理解する

診療放射線技師国家試験診療画像機器学

こんにちは！

今回は超音波ドプラ法についてまとめていきます。

といっても臨床的な話ではなく、ドプラ法の原理についてです。

ドプラ法を理解するためには、もちろんドップラー効果の理解を避けて通れません。

（超音波ドプラ法は「ドプラ」、ドップラー効果は「ドップラー」の方がよく目にするのはなぜ笑？）

ということで、ドップラー効果の復習をしてから超音波ドプラ法の原理を理解し、問題演習という形にしたいと思います。

まずはドップラー効果から復習しましょう。

ドップラー効果
超音波ドプラ法の原理
問題演習
- 第69回午後13
- 第72回午前9

ドップラー効果

ドップラー効果は音源か観測者、またはその両方が移動することにより音が変わったように聞こえる現象です。

簡単な例で言うと救急車のサイレンですね。

近づいてくる時は音が高く（周波数が高く）、遠ざかる時は音が低く（周波数が低く）聞こえます。

では、この現象を式で示してみます。

波の式

波の最も基本的な式として、

　 $v = f \lambda$

　 $v$ ：速度、 $f$ ：周波数、 $\lambda$ ：波長

があります。

意外と勘違いされることが多いのですが、この式は周波数を大きくすると速度が速くなるという意味ではありません。

高周波の音だから音速が速くなるということはありませんよね。

周波数が高くなる分、波長は短くなるので音速は変わりません。

では、基本の式を押さえたところで、ドップラー効果の式を導出してみましょう。

観測者が静止、音源が移動している場合

音源が近づいてきている場合、音源から観測者側へ向かう波は間隔が縮められます。

　　　　 f:id:Yuru-yuru:20200413182124j:plain:w400

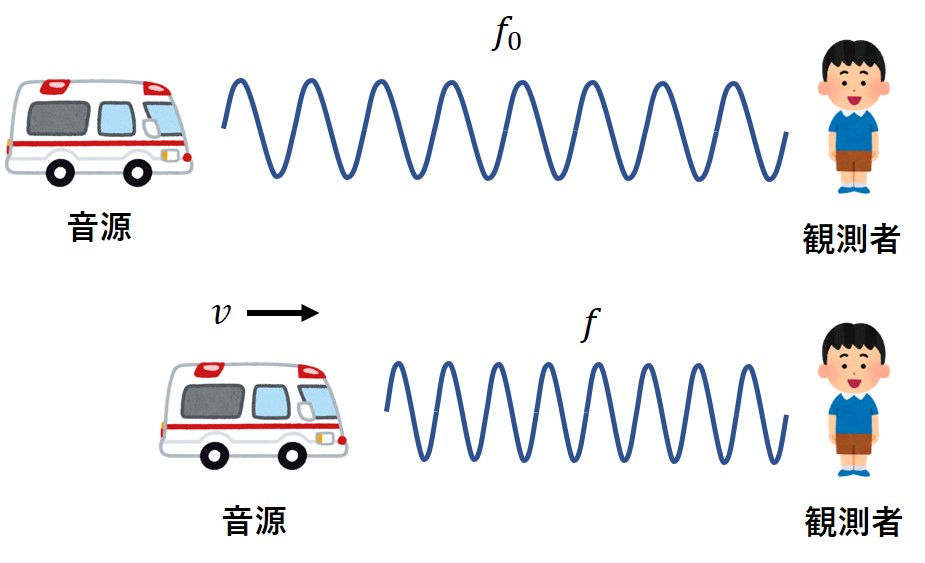
これは波長が短くなることと等しく、観測者からすると周波数が高い、すなわち音が高く感じます。

これを式で示すと、

　 $f = {\frac{c}{c-v}} \times f_0$

　 $f$ ：観測者の聞く周波数、 $c$ ：音速、 $v$ ：音源の速度、 $f_0$ ：音源の周波数

となります。

音源が静止、観測者が移動する場合

観測者が音源に近付く場合、観測者が単位時間あたりに感じる波の数は多くなるため、周波数は高くなります。

　　　　 f:id:Yuru-yuru:20200413182157j:plain:w400

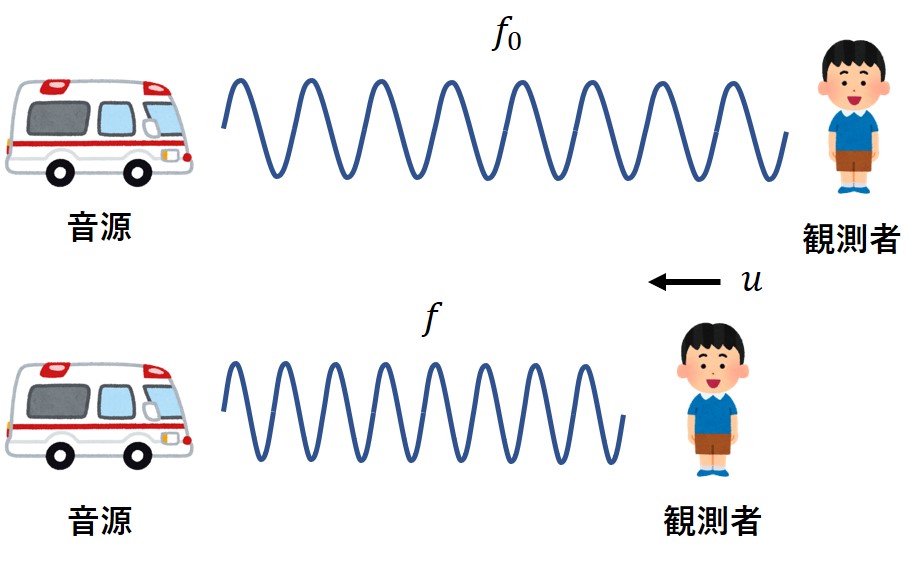
サイレンを鳴らしている救急車に向かって走っていく場面はあまりなさそうですが、観測者の速度を $u$ とすると、

　 $f = {\frac{c-(-u)}{c}} \times f_0$

と表せます。

観測者の速度は音速の方向を正としているので $-u$ となっています。

ドップラー効果の式

これら2つの式をまとめると、

　 $f = {\frac{c+u}{c-v}} \times f_0$

という形にまとめられます。

では、これらの式を用いて超音波ドプラ法の原理について考えていきましょう。

超音波ドプラ法の原理

超音波検査装置では、プローブから超音波を送信し、物体によって反射されて返ってくる超音波を受信することで画像化しています。

この過程を以下の2つに分けて考えていきます。

　1．音源（送信プローブ）が静止、観測者（反射体）が動く時、観測者が感じる周波数 $f_1$

　2．音源（反射体）が動き、観測者（受信プローブ）が静止している時、観測者が感じる周波数 $f_2$

では1つずつみていきます。

1．音源（送信プローブ）が静止、観測者（反射体）が動くとき

プローブの位置を固定して超音波を送信するため、音源は送信プローブとなります。

まずは、反射体を観測者として、反射体が観測する周波数 $f_1$ を考えていきます。

　　　　 f:id:Yuru-yuru:20200413182248j:plain:w400

先程のドップラー効果で確認した通り、音源が静止、観測者が速度 $v$ で近づいてきている場合、反射体が観測する周波数 $f_1$ は、

　 $f_1 = {\frac{c-(-v)}{c}} \times f_0$

となります。

2．音源（反射体）が動き、観測者（受信プローブ）が静止しているとき

1の過程で超音波を受け取った反射体は超音波を反射し、音源となります。

プローブが反射された超音波を受信（観測）するため、受信プローブが観測する周波数 $f_2$ を考えます。

　　　　 f:id:Yuru-yuru:20200413182310j:plain:w400

こちらも先程のドップラー効果で確認した通り、音源が速度vで近づき、観測者が静止している場合、受信プローブが観測する周波数 $f_2$ は、

　 $f_2 = {\frac{c}{c-v}} \times f_1$

　　 $= {\frac{c}{c-v}} \times {\frac{c+v}{c}} \times f_0$

　　 $= {\frac{c+v}{c-v}} \times f_0$

となります。

ドプラ偏位周波数

この式からも反射体の速度 $v$ を求めることはできますが、超音波装置では $c \gg v$ より、

　 $f_2 = \left({\frac{c+v+v}{c-v+v}} \right) \times f_0 \simeq \left(1 + {\frac{2v}{c}} \right) \times f_0$

と近似されます。

よって、

　 $f_2 \simeq f_0 + {\frac{2v}{c}} \times f_0 = f_0 + f_d$

となり、 $f_d$ はドプラ偏位周波数と呼ばれます。

$f_0$ 、 $c$ は既知、 $f_2$ を観測するため、この式から反射体の速度 $v$ を求めることができます。

しかし、超音波ドプラ法で対象となるのは主に血流であり、プローブに対して垂直に向かってくるというパターンは少ないです。

このことを考慮してもう少し変形しましょう。

実際の超音波ドプラ法

実際の超音波ドプラ法では以下のような場合が考えられます。

　　　　 f:id:Yuru-yuru:20200413182332j:plain:w200

このような場合、先程の式を用いて求められる速度 $v$ は、超音波の送信方向と平行（プローブに対して垂直）な方向の成分だけになってしまうため、

　 f:id:Yuru-yuru:20200413182955j:plain:w300

となります。

つまり、実際のドプラ偏位周波数 $f_d$ は、

　 $f_d = {\frac{2v \cos \theta}{c}} \times f_0$

と求めることができます。

やっと見覚えのある式にたどり着くことができました！

では、この式を使う問題を解いていきましょう。

問題演習

第69回午後13

13　Doppler〈ドプラ〉法において、送信周波数5 MHz、ドプラシフト周波数1 kHz、音速1,500 m/s、超音波入射方向と血管走行方向のなす角度が60度のときの血流速度［cm/s］はどれか。

　1．10

　2．20

　3．30

　4．40

　5．50

式さえ覚えていればただ代入するだけで解ける問題ですが、ここまでドプラ法の計算問題の出題がほとんどなかったようなので戸惑った方が多かったのではないかと思います。

では、再度式を確認します。

　 $f_d = {\frac{2v \cos \theta}{c}} f_0$

この式から速度 $v$ を求めると、

　 $v = {\frac{c}{2 \cos \theta}} \cdot {\frac{f_d}{f_0}}$

　　 $= {\frac{1500}{2 \times {\frac{1}{2}}}} \times {\frac{1 \times 10 ^3}{5 \times 10 ^6}}$

　　 $=0.3$ ［m/s］

　　 $=30$ ［cm/s］

となります。

解答は３ですね。

代入するだけなので簡単ですね。

少し物足りないと思うので、最新第72回の問題も解いてみましょう。

第72回午前9

9　血流方向に対して60度で超音波を送信したところ、周波数が100 ppmずれて受信された。

生体中の音速を1,500 m/sとしたとき、血流速度［cm/s］はどれか。

　1．5

　2．10

　3．15

　4．20

　5．25

先程の問題よりは少しわかりにくくなっていると思います。

「周波数が100 ppmずれている」という部分ですね。

このppmはMRIの化学シフトなどで見覚えがあると思いますが、「100万分の1」という意味です。

つまり、送信周波数 $f_0$ に対して100万分の1のズレが生じたということです。

これを考慮して問題を解いていきます。

先程の問題と同様に、

　 $v = {\frac{c}{2 \cos \theta}} \cdot {\frac{f_d}{f_0}}$

に代入します。

与えられた条件より、

　 ${\frac{f_d}{f_0}} = 100 \times 10 ^{-6} = 10 ^{-4}$

となり、代入すると、

　 $v = {\frac{1500}{2 \times {\frac{1}{2}}}} \times 10 ^{-4}$

　　 $= 0.15$ ［m/s］

　　 $=15$ ［cm/s］

と求められます。

よって解答は３になります。

どうでしょうか？

そこまで複雑な式でもないので基本的には式を覚えればよいですが、念のため導出もできるようにしておくといいかもしれないですね。

何か誤りがあれば教えてください。

ではまた！

2020-04-11

最速?!第72回国試問題解説⑥（第72回診療放射線技師国家試験午前44）

診療放射線技師国家試験放射線治療技術学

こんにちは！

今回は放射線治療技術学の重粒子線治療に関する問題です。

問題は第72回午前44です。下の解答を見る前にぜひ一度自分で考えてみてください。

（↓スマホでご覧の方は見づらくなっているので、画面を横にして見てください。）

44　重粒子線治療の深さ方向の物理線量分布の変化の組合せで正しいのはどれか。

　　入射直後のプラトー領域　　　拡大ブラッグピーク〈SOBP〉領域※

1．　　　　ほぼ一定　　　　　　　　　　　　ほぼ一定

2．　　　　ほぼ一定　　　　　　　　　　深くなるほど増加

3．　　　　ほぼ一定　　　　　　　　　　深くなるほど減少

4．　　深くなるほど増加　　　　　　　　　　ほぼ一定

5．　　深くなるほど減少　　　　　　　　　　ほぼ一定

※全然関係ないのですが、実際の問題では「ブラッグピーク」が「ブラックピーク」と書かれていました。おそらく誤字でしょう。

（第72回診療放射線技師国家試験より引用）

一見簡単そうに見えますが、重粒子線治療独特の線量計算が含まれるので少し難しかったと思います。

私も教科書のどこかで見た気がするぐらいの知識でなんとか正解できましたが、自信はありませんでした。

今回から適応された（数年前から導入されていましたが）新しい国家試験出題基準にも重粒子線の線量計算が追加されていたので、この機会に学んでおいて損はないと思います。

では、基礎知識から確認していきましょう！

重粒子線の特徴
- LETとRBE
- 線量分布（ブラッグピーク）
SOBP（拡大ブラッグピーク）
問題の解説

重粒子線の特徴

重粒子線治療はX線や電子線による治療と異なる特徴がいくつかあります。

まずは、そこから確認していきましょう。

LETとRBE

LET（Linear Energy Transfer、線エネルギー付与）は荷電粒子の飛跡に沿って単位長さ当りに局所的に与えられるエネルギー量を示します。

粒子線のLETは荷電粒子の電荷、質量が大きく、速度が遅いほど大きくなります。

放射線の線質はこのLETの違いにより、高LET放射線と低LET放射線の2つに分けられます。

知っての通り、重粒子線は高LET放射線に分類されます。

高LET放射線は放射線を照射したときの生存率

　 ${\frac{S}{S_0}} = \exp(-\alpha d-\beta d ^2)$

のうち、α成分（直線成分）が大きく、直接作用が主になります。

逆にX線や電子線などの低LET放射線は間接作用が主になっています。

このため、放射線照射による生物学的効果は高LET放射線の方が高くなります。

この生物学的効果の指標としてRBE（Relative Biological Effectiveness、生物学的効果比）があります。

RBEは基準放射線（250keVのX線）と任意の生物学的効果を与える対象の放射線の線量の比で定義されます。

より少ない線量で任意の生物学的効果を与える放射線ほどRBEが高くなるはずなので、対象の放射線の線量が分母、基準放射線の線量が分子になります。

少し注意すべきなのは、RBEはLETが100〜200 keV/μmぐらいで最大となり、それ以上LETが大きくなるとオーバーキルとなるためRBEは小さくなることです。

f:id:Yuru-yuru:20200411025120j:plain:w250

国家試験でもよく問われる部分ですね。

続いて重粒子線の線量分布について確認していきます。

線量分布（ブラッグピーク）

X線や電子線は入射表面の線量が最も大きく（正確には表面から少し奥）、表面からの深さが深くなるほど線量は小さくなっていきます。

しかし、粒子線は物質中で停止する寸前の場所で急激に線量が高くなるという分布をします。

f:id:Yuru-yuru:20200411025147j:plain:w250

これがブラッグピークと呼ばれるものですね。

これは身体深部領域の放射線治療において非常に有用な性質であることが分かると思います。

皮膚などの正常組織の線量を抑えて、深部の標的に線量を集中させられるということです。

この程度は知っているという方が多いと思いますが、もう少し確認しておくべきことがあります。

粒子線、特に重粒子線が体内に入射し減速して飛程で停止するまでの間にLETも変化しているということです。

例えば炭素線のLETは入射付近では10数 keV/µm程度であるのが、ブラッグピーク付近では100～200 keV/µmにまで上昇します。

LETがこれだけ変化するということは、その生物学的効果も大きく変化すると考えられます。

「よく考えれば確かに！」という感じではないでしょうか。

これは後々重要になってくるので頭の隅に置いておいてください。

では、最後に問題で問われているSOBP（拡大ブラックピーク）について確認していきます。

SOBP（拡大ブラッグピーク）

SOBP（拡大ブラッグピーク）は深さ方向にブラッグピークの位置をずらすようにエネルギー吸収体（リッジフィルタ）を挿入し、複数のブラッグピークを合成することによって幅を広げたものです。

f:id:Yuru-yuru:20200411025207j:plain:w300

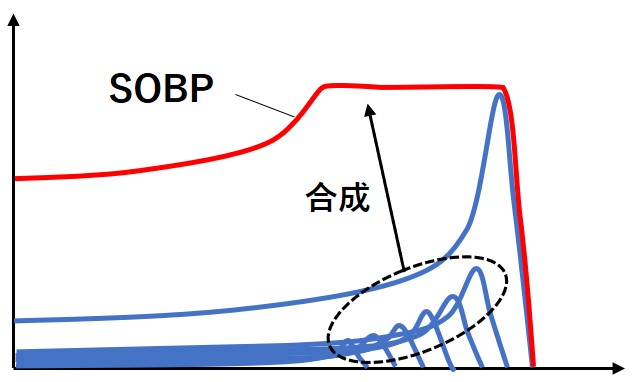
これにより標的の大きさに合わせた線量分布を作成することができるようになります。

細かい原理はスルーしておいて、何となくイメージをつかむことはできたかと思います。

ここから核心に迫っていきます。

放射線治療を行う上では標的内の線量分布を均一化する必要があります。

これは物理的な線量（物理線量）だけでなく、生物学的効果を考慮した線量分布が重要になります。

「？？？」という感じの方もおられると思いますが、もう少し詳しく書いていきます。

ここでいう物理線量は吸収線量のように放射線測定器を用いて計測できる線量のことです。

この物理線量は体内に入射したときの生物学的効果を考慮したものではありません。

実際に均一化したいのは生物学的効果を考慮した臨床線量（生物線量）のはずです。

ここで、先程のLETと生物学的効果の関係が重要になってきます。

停止直前にLETが高くなりブラッグピークを生じる重粒子線では、その位置で生物学的効果が高くなります。

これをSOBPについて考えてみましょう。

物理線量が均一になるようにSOBPを作成した場合、標的の浅い位置と深い位置で臨床線量に差が生じることが考えられます。

f:id:Yuru-yuru:20200411025228j:plain:w200

※図はイメージです。

これを避けるためには深い位置ほど物理線量を小さくする必要があります。

つまり、このような分布になります。

f:id:Yuru-yuru:20200411025253j:plain:w200

※図はイメージです。

これで標的の臨床線量を均一にすることができます。

詳しくは分かりませんが、治療計画の段階で臨床線量が一定になるように設定して、必要な物理線量を逐次近似法で最適化するようです。

ちゃんとここまで授業で習っている方もおられるかと思いますが、私は授業で聞いた覚えがなかったので少しまとめてみました。

詳しい話はもっとあると思いますが、この程度知っているだけで十分だと思います。

では、知識の確認が終わったところで、問題を解いていきます。

問題の解説

この問題では物理線量分布が問われています。

f:id:Yuru-yuru:20200411030534j:plain:w300

まず、①入射直後のプラトー領域です。

いまいち出題の意図が分からないのですが、プラトー領域だから物理線量もほぼ一定だと分かると思います。

次に②SOBP領域です。

先程確認した通り、臨床線量を均一にするためには深くなるほど物理線量が小さくなるようにする必要があります。

よって解答は３です。

最初に考えた解答と合っていたでしょうか？

少しふわっとした解説になってしまいましたが、なんとなくだけでも覚えておくと良いと思います。

何か誤りなどありましたら教えてください。

ではまた！

2020-04-09

最速?!第72回国試問題解説⑤（第72回診療放射線技師国家試験午前47）

診療放射線技師国家試験医用画像情報学画像工学

こんにちは！

今回は医用画像情報学のフーリエ変換に関する問題です。

問題は午前47です。

47　図に示す余弦関数をFourier〈フーリエ〉変換した結果で正しいのはどれか。2つ選べ。

　　1．0［cycles/mm］の成分は0.0である。

　　2．1［cycle/mm］の実数部は1.0である。

　　3．1［cycle/mm］の虚数部は1.0である。

　　4．－1［cycle/mm］の実数部は1.0である。

　　5．－1［cycle/mm］の虚数部はー1.0である。

フーリエ変換の性質として知っていた方は特別難しいと思わなかったかもしれませんが、これを理解するのはなかなか難しいと思います。

また、最近の傾向なのか分かりませんが、「ちゃんとフーリエ変換分かってますか？」という感じの問題が多い感じがします。

数年前まではお決まりの問題しか出ていなかったみたいですけどね。

そんなことはどうでもいいのですが、とにかくフーリエ変換を理解しておくことは重要です。

なんとなくの意味は分かっている方がほとんどだと思うので、とりあえず計算ができるように頑張りましょう。

ではまず、フーリエ変換の基礎から確認していきましょう！

基礎知識の確認
問題の解説
おまけ
まとめ

基礎知識の確認

画像工学分野におけるフーリエ変換は画像を構成する信号を空間周波数ごとに扱うために用いられます。

高周波の成分を強調することで鮮鋭度を上げたり、逆に抑制することで平滑化したりなど様々な処理が行われます。

では、このフーリエ変換とはどのような計算が行われるのでしょうか。

フーリエ変換

画像データのような2次元の関数を考えるとややこしくなるので、1次元の関数について考えます。

1次元の関数 $f(x)$ のフーリエ変換 $F(\omega)$ は以下の式で表されます。

　 $F(\omega) = \int_{-\infty} ^{\infty} f(x) e ^{-i \omega x} dx$

式を見てもなぜこれが空間周波数の関数になるかわからないと思いますが、そこまで掘るとかなり長くなるので今回はスルーさせてください笑

とりあえずこの式を認めて、どのように計算処理が行われるのかを理解しましょう。

オイラーの公式

このフーリエ変換の計算を行っていくうえでオイラーの公式を覚えておく必要があります。

　 $e ^{i \theta} = \cos{\theta} + i \sin{\theta}$

この式自体は数IIIまでやっていれば見たことがあると思います。

先程のフーリエ変換の式にeが含まれるのも実はこの式が関係しています。

今回は $\theta = \omega x$ として

　 $e ^{i \omega x} = \cos(\omega x) + i \sin(\omega x)$

という式を主に使っていきます。

δ関数の性質

cos波をフーリエ変換する中で、δ関数の性質を使う場面がでてきます。

なので、必要となるδ関数の性質について少し確認しておきましょう。

せっかく勉強したので軽く説明も書きますが、式だけ少し見て後はさらっと読み飛ばすぐらいで大丈夫です。

まず、δ関数とは以下のようなものです。

f:id:Yuru-yuru:20200409184502j:plain:w400

詳しいことは省きますが正確に定義するならば、

　 $\int_{-\infty} ^{\infty} f(x) \delta (x) dx = f(0)$

となるようです。これはδ関数をx軸に平行移動した場合にも同様に成り立ち、

　 $\int_{-\infty} ^{\infty} f(x) \delta (x-a) dx = f(a)$

となります。

$f(x)$ にδ関数を掛けて積分すると、そのδ関数の位置の $f(x)$ の値が出力されるということですね。

この性質を利用して、δ関数のフーリエ変換を求めることもできます。

$f(x) = e ^{-ikx}$ とすると、先程の式より、

　 $\int_{-\infty} ^{\infty} \delta (x-a) e ^{-ikx} dx = e ^{-ika}$

となり、これが成り立つならば右辺を逆フーリエ変換すれば $\delta(x-a)$ になるはずです。

よって、

　 $\delta(x-a) = {\frac{1}{2 \pi}} \int_{-\infty} ^{\infty} e ^{-ika} \cdot e ^{ikx} dk$

　　　　　 $= {\frac{1}{2 \pi}} \int_{-\infty} ^{\infty} e ^{ik(x-a)} dk$

となります。

今の時点ではこれが一体何の役に立つんだという感じだと思いますが、後々使うので出てきたらここに戻って確認してください。

最後にδ関数の対称性についてです。

これは偶関数と同じような性質であり、式で示すと、

　 $\delta(x) = \delta(-x)$

です。

原点を中心として線対称になるということですね。

基礎知識としてはこの程度で大丈夫だと思います。

では、問題を解いていきましょう！

問題の解説

先程示した通り、問題では周期が1 mmの余弦関数（コサイン）をフーリエ変換することが求められています。

f:id:Yuru-yuru:20200409172351j:plain:w500

ここで計算を始める前に、フーリエ変換が信号を周波数ごとに分解する（周波数の関数に変換する）ものであることを思い出してください。

図を見る限り周期が一定、すなわち周波数が一定の余弦関数なのでフーリエ変換すると、この余弦関数の周波数にある値を持つことは分かると思います。

このことを頭に置いたうえで計算してみましょう。

フーリエ変換の式を再掲します。

　 $F(\omega) = \int_{-\infty} ^{\infty} f(x) e ^{-i \omega x} dx$

今回は $f(x) = \cos(\omega_0 x)$ なので、これを代入して計算していきます。

　 $F(\omega) = \int_{-\infty} ^{\infty} \cos (\omega_0 x) e ^{-i \omega x} dx$

ここで $\cos(\omega_0 x)$ としたのは、 $f(x)$ は $\omega$ が変数ではなく固定された値であるためです。

さて計算しよう！というところで、いきなり先程のオイラーの公式を用いる必要があります。

オイラーの公式より

　 $e ^{i \omega x} = \cos(\omega x) + i \sin(\omega x)$

　 $e ^{-i \omega x} = \cos(\omega x) - i \sin(\omega x)$

が成り立つため、

　 $e ^{i \omega x} + e ^{-i \omega x} =2 \cos(\omega x)$

　 $cos(\omega x) = {\frac{e ^{i \omega x} + e ^{-i \omega x}}{2}}$

と表せるため、先程の $F(\omega)$ は、

　 $F(\omega) = \int_{-\infty} ^{\infty} \left({\frac{e ^{i \omega_0 x} + e ^{-i \omega_0 x}}{2}}\right) e ^{-i \omega x} dx$

　　　　 $= {\frac{1}{2}} \int_{-\infty} ^{\infty} \left(e ^{i(\omega_0 -\omega) x} + e ^{-i (\omega_0 + \omega) x}\right) dx$

ここで先程のδ関数の性質を使用します！

　 $\delta(x-a) = {\frac{1}{2 \pi}} \int_{-\infty} ^{\infty} e ^{ik (x-a)} dk$

この式を使っていきます。

先程の式を眺めると、上式の右辺に似た形があることが分かると思います。

よって各項に分けて計算すると、

　 $\pi \delta(\omega_0 - \omega) = {\frac{1}{2}} \int_{-\infty} ^{\infty} e ^{i(\omega_0 - \omega) x} dx$

　 $\pi \delta(-\omega_0 -\omega) = {\frac{1}{2}} \int_{-\infty} ^{\infty} e ^{-i(\omega_0 + \omega) x} dx$

となります。

まとめると、

　 $F(\omega) = \pi \delta(\omega_0 - \omega) + \pi \delta(-\omega_0 -\omega)$

δ関数の対称性より

　 $F(\omega) = \pi \{\delta(\omega - \omega_0) + \delta(\omega + \omega_0)\}$

これより $\omega = \omega_0 , -\omega_0$ で正の値を取る実数であることが分かります。

f:id:Yuru-yuru:20200409190316j:plain:w300

これで一応問題の解答は出来るかと思います。

解答は２と４です。

この値が1になるというのは私もイマイチ分かっていないので、誰か分かったら教えてください笑

では、おまけで正弦波（sin波）についてもやってみましょう！

おまけ

基本的にはcos波と同様です。

$f(x) = \sin (\omega_0 x)$ とすると、フーリエ変換 $F(\omega)$ は、

　 $F(\omega) = \int_{-\infty} ^{\infty} \sin (\omega_0 x) e ^{-i \omega x} dx$

ここでオイラーの公式より、

　 $sin(\omega_0 x) = {\frac{e ^{i \omega_0 x} - e ^{-i \omega_0 x}}{2i}}$

であるため、 $F(\omega)$ は、

　 $F(\omega) = \int_{-\infty} ^{\infty} \left({\frac{e ^{i \omega_0 x} - e ^{-i \omega_0 x}}{2i}}\right) e ^{-i \omega x} dx$

　　　　 $= {\frac{1}{2i}} \int_{-\infty} ^{\infty} \left(e ^{i(\omega_0 -\omega) x} - e ^{-i (\omega_0 + \omega) x}\right) dx$

　　　　 $= {\frac{i}{2}} \int_{-\infty} ^{\infty} \left(e ^{-i(\omega_0 +\omega) x} - e ^{i (\omega_0 - \omega) x}\right) dx$

となる。先程と同様、δ関数の式より、

　 $F(\omega) = \pi i \delta(-\omega_0 - \omega) - \pi i \delta(\omega_0 -\omega)$

δ関数の対称性より、

　 $F(\omega) = \pi i \{\delta(\omega + \omega_0) - \delta(\omega - \omega_0)\}$

これより、 $\omega = -\omega_0$ で正の値、 $\omega = \omega_0$ で負の値を取る純虚数であることがわかります。

f:id:Yuru-yuru:20200409190416j:plain:w300

これは偶関数であるcos波のフーリエ変換が実数、奇関数であるsin波のフーリエ変換が純虚数となることに一致しています。

まとめ

少々ややこしい計算もありましたが、何とか理解できたでしょうか？

実際には知識として押さえておくのが良いと思います。

試験中にフーリエ変換の計算をするのはかなり面倒臭いですよね笑

自信がない時に確かめる意味でやってみてもいいかもしれません。

さも全て分かったように書いていますが、曖昧な部分もあるのでもっと詳しい方がいらっしゃったらぜひ補足してくさい！

ではまた！

2020-04-05

最速?!第72回国試問題解説④（第72回診療放射線技師国家試験午前8）

診療放射線技師国家試験診療画像機器学医用工学

こんにちは！

今回は診療画像機器学のインバータ式X線装置に関する問題です。

問題は午前8です。

8　共振形インバータ式X線装置で正しいのはどれか。

　　1．並列共振形は大容量X線装置に適している。

　　2．大負荷になるほどインバータ周波数が高くなる。

　　3．スイッチング時の電力損失は非共振形より大きい。

　　4．直列共振形は負荷抵抗が大きいほど電流の変化が大きい。

　　5．並列共振形は負荷抵抗が小さいほど共振現象を利用しやすい。

どうでしょうか？

インバータについてそこそこ分かっている方でも戸惑う問題だと思います。

まず、選択肢の意味がよく分からない笑

正答を選べた人もなんとなく合ってるっぽいぐらいの感覚だと思います。

今回は各選択肢について、その基礎となる知識を確認しながら解いていきます。

かなり重めですが、気になる人はぜひ最後まで読んでみてください。

問題の解説

選択肢を大きく分けると、

1、4、５　→　直列共振と並列共振

2　→　インバータ周波数

3　→　スイッチング損失

と分けられます。

それぞれについて見ていきましょう。

直列共振と並列共振

共振についてはなんとなく理解している方が多いと思います。

よく分からない方は以下の記事をご覧ください。

yuruyurudokugaku.hatenablog.jp

共振回路は抵抗、コンデンサ、コイルの接続方式によって直列共振と並列共振に分けられます。

まずは、直列共振から見ていきます。

直列RLC回路のインピーダンスZは、

　 $Z = R + j \left(\omega L - {\frac{1}{\omega C}}\right)$

と表せます。

共振状態ではインピーダンスZが最小になるため、

　 $\omega L - {\frac{1}{\omega C}} = 0$

となり、この時共振周波数 $f_0$ は、

　 $\omega_0 = {\frac{1}{\sqrt{LC}}}$

　 $f_0 = {\frac{1}{2 \pi \sqrt{LC}}}$

となります。

共振形インバータ式装置ではこの周波数（インバータ周波数）を変えることで出力の調整をしています。

では、次に並列共振を見ていきます。

先程と同様にインピーダンスZを求めようとすると少しややこしい式になるので、多くの場合インピーダンスの逆数であるアドミタンスYを用います。

並列共振回路のアドミタンスYは、

　 $Y = {\frac{1}{R}} + j \left(\omega C - {\frac{1}{\omega L}}\right)$

となります。

共振状態ではこのアドミタンスYが最小となるため、

　 $\omega C - {\frac{1}{\omega L}} = 0$

となり、共振周波数は直列共振と等しくなります。

少し注意が必要なのは、並列共振ではアドミタンスが最小となることです。

アドミタンスはインピーダンスの逆数であり、電流の流れやすさを示すものですから、並列共振の時流れる電流は最小になります。

基本はこの程度です。

では、各選択肢を見ていきます。

1．並列共振形は大容量X線装置に適している。

早速「そんなの知るか！」という感じの選択肢ですね笑

これは直列共振と並列共振それぞれの共振特性を理解している必要があります。

後程他の選択肢でも出てくるのですが、「共振特性を利用しやすい」とは、共振曲線の尖鋭度（Q値）が大きいことを示しています。

ではここで、直列共振のインピーダンスの式を見てみましょう。

　 $Z = R + j \left(\omega L - {\frac{1}{\omega C}}\right)$

Rが小さいほどZが小さくなるため、Rが小さいほど共振特性を利用しやすいということになります。

Rが小さいということは電流を大きくすることができ、大容量X線装置に適していると考えられます。

次に並列共振のアドミタンスの式を見ると、

　 $Y = {\frac{1}{R}} + j \left(\omega C - {\frac{1}{\omega L}}\right)$

並列共振ではRが大きい方がYが小さくなるため、Rが大きいほど共振特性を利用しやすいということになります。

訂正：上図に誤りがあります。正しくは

　　　R 小　→　Q 小　R大　→　Q大　

Rを大きくすると電流に制限がかかるため、大容量X線装置に適しているとは言えません。

ということで、この選択肢は誤りになります。

1つ目からなかなかわかりにくい選択肢ですが、これが分かれば後の2つは簡単です。

4．直列共振形は負荷抵抗が大きいほど電流の変化が大きい。

5．並列共振形は負荷抵抗が小さいほど共振現象を利用しやすい。

これらは先ほど書いた通り、直列共振は抵抗が小さいほど、並列共振は抵抗が大きいほど共振現象を利用しやすいため誤りと分かります。

では、次に行きましょう。

インバータ周波数

インバータ周波数とはインバータによるスイッチングの周波数です。

ここでは2の選択肢について考えます。

2．大負荷になるほどインバータ周波数が高くなる。

これは主に共振形インバータ装置のことだと思いますが、大負荷、つまり大管電流の場合にインバータ周波数がどうなるか問われています。

共振特性のグラフを見てもらえば分かると思いますが、共振形インバータ式装置ではインバータ周波数を高くする（共振周波数に近づける）ことで電流を大きくできます。

この単純な理由からもこの選択肢が正しいことを判断できると思いますが、もう少し考えてみましょう。

インバータ回路を通して交流となった電流はコンデンサなどの平滑化回路を通ることで最終的な管電圧波形となります。

この平滑化回路は電流が大きくなると、その平滑効果が小さくなってしまいます。

つまりリプル百分率が大きくなってしまうということです。

しかし、先ほども言ったように共振形インバータでは電流を大きくするためにインバータ周波数を高くする必要があるので、リプル百分率を小さく抑えることができます。

この点でもやはり大負荷の場合にインバータ周波数は高くなると考えられるでしょう。

では、最後にスイッチング損失について押さえましょう。

スイッチング損失

まず、スイッチング損失について確認していきます。

インバータ装置などで行われるスイッチングには主に半導体素子が使われています。

このスイッチング素子がON（オン）のとき、半導体には電流が流れます。

半導体にも内部抵抗があるので、電流が流れているときも素子の両端には電位差（電圧）がありますが、大きさは小さいものです。

逆にスイッチング素子がOFF（オフ）のとき、半導体には電流が流れません（正確には漏洩電流がありますが）。

電流が流れないので素子の両端にかかる電圧が大きくなります。

では、スイッチングを行ったその瞬間には流れる電流と素子の両端にかかる電圧はどうなっているでしょうか。

理想的にはスイッチングは方形波（矩形波）で行われますが、実際には完全にオン・オフになるために少し時間がかかります。

図で示すと、

このようにスイッチングの瞬間には流れる電流と素子の両端電圧の両方が高くなってしまいます。

この電圧・電流によって生じる熱損失がスイッチング損失です。

スイッチング損失はスイッチングにかかる時間が長く、スイッチングの周波数が高いほどこの損失が大きくなってしまいます。

スイッチング損失について簡単に理解したところで問題の選択肢を見ていきます。

3．スイッチング時の電力損失は非共振形より大きい。

共振形と非共振形でスイッチング損失を比較する必要がありますね。

当たり前ですが、共振形と非共振形の大きな違いは共振回路が含まれているかどうかです。

この共振回路に含まれるコンデンサやコイルなどによりスイッチがオン状態になった瞬間には電流がほとんど流れません。

これによりスイッチング時の損失が少ないという特徴があります。

よってこの選択肢は誤りとなります。

まとめ

インバータ式装置についての問題でしたが、選択肢に関する内容だけを抜粋して解説したので少し分かりにくかったかもしれません。

もう少し基礎から理解したいという方は以下の記事をご覧ください。

yuruyurudokugaku.hatenablog.jp

何か誤りがありましたら教えてください。

ではまた！

2020-04-01

最速?!第72回国試問題解説③（第72回診療放射線技師国家試験午前4）

診療放射線技師国家試験放射化学

こんにちは！

今回は放射化学の溶媒抽出法に関する問題です。

問題は午前4です。

4　溶媒抽出法で抽出率を求める式はどれか。

ただし、分配比（＝有機相中の放射性核種の全濃度/水相中の放射性核種の全濃度）を $D$ 、有機相の体積を $V_0$ 、水相の体積を $V_w$ とする。

　　1． $D / (D + V_o / V_w)$

　　2． $D / (D + V_w / V_o)$

　　3． $D \cdot (1 / D + V_o / V_w)$

　　4． $D \cdot (1 / D + V_w / V_o)$

　　5． $D / (D + 1 / (V_w \cdot V_o) )$